चित्र में ΔABC का अन्तः वृत्त , भुजाओं BC, CA और AB को क्रमशःबिंदुओं D ,E और F पर स्पर्श करता है । सिद्ध करो कि
AF+BD+CE=AE+CD=12(ΔABC का परिमाप)
चूँकि बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं कि लम्बाईयाँ समान होती हैं । अतः
AF =AE … (i)
BD=BF … (ii)
तथा, CE =CD … (iii)
(i) (ii) और (iii) को जोड़ने पर
AF+BD+CE=AE+BF+CD … (iv)
∴ΔABC का परिमाप =AB+BC+CA
⇒ΔABC का परिमाप =(AF+BF)+(BD+CD)+(AE+CE)
⇒ΔABC का परिमाप =(AF+AE)+(BF+BD)+(CD+CE)
⇒ΔABC का परिमाप =2AF+2BD+2CE [ (i) (ii) और (iii) से AF=AE,BF,BD,CE=CD]
अतः ΔABC का परिमाप =2(AF+BD+CE)
⇒AF+BD+CE=12(ΔABCका परिमाप)
परन्तु AF+BD+CE=AE+BF+CD [(iv)) से]
अतः AF+BD+CE=AE+BF+CD=12(ΔABC का परिमाप)

Topper's Solved these Questions
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.1
4 Videos
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.2
22 Videos
- वास्तविक संख्याएँ BOOK - RD SHARMACHAPTER - वास्तविक संख्याएँ EXERCISE - बहु विकल्पीय प्रश्न
25 Videos
- वृत्तों से सम्बन्धित क्षेत्रफल BOOK - RD SHARMACHAPTER - वृत्तों से सम्बन्धित क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
45 Videos
Similar Questions
रिक्त स्थानों की पूर्ति कीजिए :
(i) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को कहते ………. हैं।
(ii) एक वृत्त की ..... समानान्तर स्पर्श रेखाएँ हो सकती हैं ।
(iii) किसी वृत्त की स्पर्श रेखा उसे ..... बिंदुओं पर प्रतिच्छेद करती है ।
(iv) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को कहते हैं ।
(v) वृत्त पर स्पर्श रेखा के स्पर्श बिन्दु तथा उस बिन्दु से गुजरने वाली त्रिज्या के बीच का कोण ...... का होता है ।
View Solutionयदि किसी वृत्त C(O,r) पर PT स्पर्श रेखा है तथा OP=17 सेमी और OT =8 सेमी हो , तो स्पर्श रेखा की लम्बाई ज्ञात करो ।
View Solution144 के अभाज्य गुणनखण्डों में 2 की घात है :
View Solutionएक वृत्त की परिधि तथा क्षेत्रफल रूप से समान हों, तो वृत्त का व्यास है :
View SolutionIn the given figure, D, E and F are the points where the incircle of the DeltaABC touches F the sides BC, CA and AB respectively. Show that AF+ BD + CE = AE + BF + CD = (perimeter of Delta ABC)
View SolutionIf D,EandF are three points on the sides BC,CAandAB, respectively, of a triangle ABC such that the BDCD,CEAE,AFBF=−1
View SolutionIn Fig. 10.19, the incircle of ABC touches the sides BC, CA and AB at D, E and F respectively. Show that AF+BD+CE=AE+BF+CD=12(Perimeter of ABC) (FIGURE)
View SolutionΔABC के अंदर बिंदु O से भुजाओ BC,CA और AB पर क्रमशः लंब OD,OE और OF डाले गए है । सिद्ध कीजिए कि AF2+BD2+CE2=AE2+CD2+BF2.
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

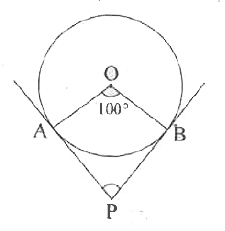
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
View Solutionभूमिका | वृत्त का परिमाप और क्षेत्रफल | उदाहरण
View SolutionDeltaABC The inner circle touches the sides BC, CA and AB on D, E and F respectively. Prove that AF+BD+CE=AE+CD+BF=1/2(DeltaABC The perimeter of )
View SolutionIn ΔABC, the incircle touches the sides BC, CA and AB, respectively, at D, E,and F. If the radius of the incircle is 4 units and BD, CE, and AF are consecutive integers, then
View SolutionIn Fig. the incircle of △ABC, touches the sides BC, CA and AB at D, E respectively. Show that : AF + BD + CE = AE + BF + CD = ½ (Perimeter of △ABC).
View SolutionA circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is: एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View Solution
