चित्र में,l और m, एक वृत्त पर बिंदुओं A और B पर दो समानान्तर स्पर्श रेखाएँ हैं। यदि वृत्त पर बिंदु पर खींची गई स्पर्श रेखा , स्पर्श रेखाओं l और m के बीच DE अन्तः खण्ड काटती हैं और F वृत्त का केंद्र हैं ,तो सिद्ध करो कि ∠DEF=90∘
स्पष्ट है कि बिंदु से और वृत्त पर दो स्पर्श रेखाएँ हैं जोकि D को वृत्त के केंद्र F से मिलाने वाली रेखा DF से सामान कोण बनाती है अर्थात
∠CDF=∠ADF
परन्तु ∠ADC=∠ADF=∠CDF
⇒∠ADC=2∠CDF
बाह्य बिंदु E से EB और EC वृत्त पर दो स्पर्श रेखाएँ हैं । अतः EB और EC ,EF से समान कोण बनायेंगी|
अर्थात ∠BEF=∠CEF ... (iii)
⇒∠BEC=2∠CEF [∵∠BEC=∠BEF+∠CEF]
चूंकि l||m हैं । अतः तिर्यक रेखा DE के एक ही ओर बने अन्तः कोणों का योग होगा अर्थात
∠ADE+∠BED=180∘
⇒∠ADC+∠BEF=180∘
⇒2∠CDF+2∠CEF=180∘
⇒2{∠CDF+∠CEF}=180∘
⇒∠CDF+∠CEF=90∘
ΔDEF में कोण योग गुणधर्म लगाने पर
∠CDF+∠CEF+∠DEF=180∘
⇒90∘+∠DEF=180∘ [(iii) से]
⇒∠DEF=90∘

Topper's Solved these Questions
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.1
4 Videos
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.2
22 Videos
- वास्तविक संख्याएँ BOOK - RD SHARMACHAPTER - वास्तविक संख्याएँ EXERCISE - बहु विकल्पीय प्रश्न
25 Videos
- वृत्तों से सम्बन्धित क्षेत्रफल BOOK - RD SHARMACHAPTER - वृत्तों से सम्बन्धित क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
45 Videos
Similar Questions
रिक्त स्थानों की पूर्ति कीजिए :
(i) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को कहते ………. हैं।
(ii) एक वृत्त की ..... समानान्तर स्पर्श रेखाएँ हो सकती हैं ।
(iii) किसी वृत्त की स्पर्श रेखा उसे ..... बिंदुओं पर प्रतिच्छेद करती है ।
(iv) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को कहते हैं ।
(v) वृत्त पर स्पर्श रेखा के स्पर्श बिन्दु तथा उस बिन्दु से गुजरने वाली त्रिज्या के बीच का कोण ...... का होता है ।
View Solutionयदि किसी वृत्त C(O,r) पर PT स्पर्श रेखा है तथा OP=17 सेमी और OT =8 सेमी हो , तो स्पर्श रेखा की लम्बाई ज्ञात करो ।
View Solution144 के अभाज्य गुणनखण्डों में 2 की घात है :
View Solutionएक वृत्त की परिधि तथा क्षेत्रफल रूप से समान हों, तो वृत्त का व्यास है :
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
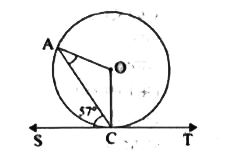
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solution3सेमी त्रिज्या वाले वृत्त पर स्थित किसी बिंदु पर स्पर्श रेखा की रचना कीजिए।
View Solution2.6 सेमी त्रिज्या का एक वृत्त खींचिए। इस पर कोई बिंदु P से लेकर उस पर एक स्पर्श रेखा खींचिए।
View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solutionखण्ड 'अ'खण्ड 'ब'1.वृत्त के अन्तः बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(a)समकोण2.वृत्त के किसी बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(b)स्पर्श रेखा3.वृत्त के बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखाओं की संख्या(c)शून्य4.स्पर्श रेखा और स्पर्श बिंदु से जाने वाली त्रिज्या के बीच बना कोण(d)एक5.वृत्त को केवल एक बिंदु पर प्रतिच्छेद करने वाली रेखा(e)दो
View Solutionरचना -3 (वृत्त पर स्पर्श रेखाएँ खींचना )
View Solutionकिसी वाह्य बिंदु से वृत्त पर स्पर्श रेखाओं की रचना
View Solution
