A तथा B केंद्रों वाले दो वृत्त जिनकी त्रिज्याएँ क्रमशः 3 सेमी. है, परस्पर दो बिंदुओं C तथा D पर इस प्रकार काटती हैं कि AC तथा BC इन दो व्रतों कि स्पर्श रेखाएँ हैं । उभयनिष्ठ जीवा CD कि लम्बाई ज्ञात करें ।
चूँकि वृत्त के एक बिंदु पर स्पर्श रेखा , स्पर्श बिंदु कि त्रिज्या लम्बवत होती है । अर्थात
∠ACB=90∘

अब ΔACB में
AB2=AC2+BC2 [पाइथोगोरस प्रमेय से ]
⇒AB2=32+42=9+16=25
⇒AB=5 सेमी.
चूँकि परस्पर प्रतिच्छेद करने वाले दो व्रतों के केन्द्रों को मिलाने वाली रेखा , उनके उभयनिष्ठ जीवा पर लम्ब समद्विभाजक होती है।
∴AP⊥CD तथा CP=PD
मान लें AP=x तो, BP =5-x " " [∵AB=5cm]
पुनः मान लें, CP =DP =y सेमी.
ΔAPC तथा ΔBPC में पाइथोगोरस प्रमेय के उपयोग से , हम देखते हैं कि
AC2=AP2+PC2,BC2=PB2+PC2
⇒32=x2+y2 तथा 42=(5−x)2+y2
⇒42−32={(5−x)2+y2}−{x2+y2}
⇒7=25−10x
⇒10x=18⇒x=1.8 सेमी.
∴32=x2+y2⇒y=√9−(1.8)2=√5.76=2.4 सेमी.
अतः CD =2CP =2y =4.8 सेमी.
Topper's Solved these Questions
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.1
4 Videos
- वृत्त BOOK - RD SHARMACHAPTER - वृत्त EXERCISE - प्रश्नावली 10.2
22 Videos
- वास्तविक संख्याएँ BOOK - RD SHARMACHAPTER - वास्तविक संख्याएँ EXERCISE - बहु विकल्पीय प्रश्न
25 Videos
- वृत्तों से सम्बन्धित क्षेत्रफल BOOK - RD SHARMACHAPTER - वृत्तों से सम्बन्धित क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
45 Videos
Similar Questions
रिक्त स्थानों की पूर्ति कीजिए :
(i) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिन्दु को कहते ………. हैं।
(ii) एक वृत्त की ..... समानान्तर स्पर्श रेखाएँ हो सकती हैं ।
(iii) किसी वृत्त की स्पर्श रेखा उसे ..... बिंदुओं पर प्रतिच्छेद करती है ।
(iv) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को कहते हैं ।
(v) वृत्त पर स्पर्श रेखा के स्पर्श बिन्दु तथा उस बिन्दु से गुजरने वाली त्रिज्या के बीच का कोण ...... का होता है ।
View Solutionयदि किसी वृत्त C(O,r) पर PT स्पर्श रेखा है तथा OP=17 सेमी और OT =8 सेमी हो , तो स्पर्श रेखा की लम्बाई ज्ञात करो ।
View Solution144 के अभाज्य गुणनखण्डों में 2 की घात है :
View Solutionएक वृत्त की परिधि तथा क्षेत्रफल रूप से समान हों, तो वृत्त का व्यास है :
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionदो वृत्त एक -दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ कि संख्या लिखिए।
View Solutionदिये गये चित्र में O वृत्त का केंद्र है। AB व AC वृत्त कि स्पर्श रेखाएं है। यदि OA=10 सेमी तथा OB=6 सेमी है तो AC कि लम्बाई लिखिए।
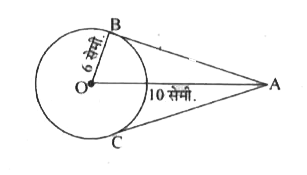
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionदो वृत्त जिनकी त्रिज्याएँ क्रमशः 2.5 सेमी एवं 1.5 सेमी है जिनके केंद्र 8 सेमी दूरी पर स्थित है ,पर एक उभयनिष्ठ तिर्यक स्पर्श रेखा किन रचना कीजिए।
View Solutionदो वृत्त जिसकी त्रिज्याएँ 3 सेमी एवं 4 सेमी है। जिनके केन्द्रो के बाध्य की दूरी 8 सेमी है। दोनों वृतो पर उभयनिष्ठ स्पर्श रेखाएं कीतिनि खींची जा सकती है ?तथा दो उभयनिष्ठ अनुस्पर्श रेखाओ की रचना कीजि।
View Solutionएक 4 सेमी त्रिज्या का वृत्त खींचिए। उस पर दो स्पर्श रेखाएं इस प्रकार खींचिए कि वे परस्पर 70∘ का कोण बनती हो।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionदो वृत्त जिनकी त्रिज्याएँ 4 सेमी और 3 सेमी है तथा दोनों के केन्द्रो कि मध्य दूरी 6.5 सेमी हैकि रचना कर उन पर एक उभयनिष्ठ अनुस्पर्श रेखा कि रचना कीजिए।
View Solution2.5 सेमी का एक वृत्त खींचिए। वृत्त के केंद्र से 6.5 सेमी कि दूरी पर स्थित किसी बिंदु से वृत्त कि स्पर्श रेखाएं खींचिए। स्पर्श रेखाओ कि लम्बाई नापकर तथा गणना द्वारा ज्ञात कीजिए।
View Solutionदो वृत्त 2.5 सेमी एवं 1 सेमी त्रिजियो के केंद्र परस्पर 7 सेमी दूरी पर है। एक उभयनिष्ठ तिर्यक स्पर्श रेखा कि रचना कीजिए।
View Solution
