दवा का एक केप्सूल (capsule) एक बेलन के आकर का है जिसके दोनों सिरों पर चित्र 16.53 के अनुसार , एक - एक अर्द्धगोला लगा है | पूरे केप्सूल की लम्बाई 14 मिमी . और इसका व्यास 15 मिमी है | इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
बेलनाकार भाग के लिए ,
r = त्रिज्या =52 मिमी = 2 .5 मिमी
∴ S1 बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल
⇒ S1=2πrh
⇒ S1=2×227×2.5×9मिमी2
तथा दो अर्द्धगोली भाग के लिया
r = त्रिज्या = 2 .5 मिमी .
∴ दो अर्द्धगोलिया भाग का व्रक पृष्ठीय क्षेत्रफल =2×2πr2=4πr2=4×227×(2.5)2मिमी2
अतः केप्सूल का कुल पृष्ठीय क्षेत्रफल ={2×227×2.5×9+4×227×(2.5)2}मिमी2
=2×227×2.5(9+2×2.5)मिमी2
=2×227×2.5×14मिमी2
=2×22×2.5×2मिमी2=220मिमी2

Topper's Solved these Questions
- पृष्ठीय क्षेत्रफल और आयतन BOOK - RD SHARMACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - प्रश्नावली 16.1
42 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - RD SHARMACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - प्रश्नावली 16.2
21 Videos
- निर्देशांक ज्यामिति BOOK - RD SHARMACHAPTER - निर्देशांक ज्यामिति EXERCISE - बहु विकल्पीय प्रश्न
40 Videos
- प्रायिकताBOOK - RD SHARMACHAPTER - प्रायिकताEXERCISE - बहु विकल्पीय प्रश्न
29 Videos
Similar Questions
एक 8 सेमी. त्रिज्या के सीसे के ठोस गोले से 1 सेमी. त्रिज्या की कितनी गोलियाँ बनायी जा सकती हैं?
View Solutionएक बेलनकर्ता टेन्ट का ऊपरी हिससा शक्वाकार है | बेलन का व्यास 24 मीटर तथा शक्वाकार हिस्से की उचाई 11 मीटर है यदि शकु की शीर्ष जमीन से 16 मीटर उचाई पर हो , तो टेन्ट में लगने वाले केनवास (कपड़े ) का क्षेत्रफल ज्ञात करे |
View Solutionबिन्दुओं (cosθ,sinθ) तथा (sinθ,−cosθ) के बीच की दूरी है :
View Solutionयदि अंको 1, 2,3,4,5,6,7,8,9 में से एक अंक यादृच्छया चुना जाता है, तो एक विषम अंक प्राप्त होने की प्राविकता है:
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक परवलय के नाभिलम्ब का समीकरण x+y=8 तथा उसके शीर्ष पर स्पर्शी का समीकरण x+y=12 है, तो उसके नाभिलम्ब की लम्बाई है :
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
View Solutionआकलन एक सतत् प्रक्रिया है। इसका प्राथमिक उद्देश्य है
View Solutionएक मशीन का मूल्य 7500 रुo है। इसका मूल्य 5% वार्षिक दर से घट रहा है तब एक वर्ष बाद इसका मूल्य क्या होगा?
View SolutionThe radius of circle is a side of a square. The ratio of the areas of the circle and the square is. एक वृत्त की त्रिज्या एक वर्ग की भुजा है। वृत्त और वर्ग के क्षेत्रफलों का अनुपात है
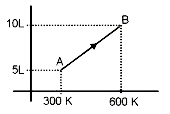
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
View Solution
