एक समतल में 10 बिंदु हैं, इसमें कोई भी तीन एक सरल रेखा पर स्थित नहीं हैं केवल उन 4 बिन्दुओं को छोड़कर जो संरेखीय हैं । ज्ञात कीजिए -
(i) बिन्दुओं के युग्म से बनने वाली सरल रेखाओं की संख्या ।
(ii) इन बिन्दुओं को शीर्ष बनाने वाले त्रिभुजों की संख्या ।
(i) 10 बिंदुओं से 2-2 बिंदु लेकर बनने वाली सरल रेखाओं की संख्या
=10C2=10!2!×8!=45
4 संरेखीय बिंदुओं में से एक समय 2-2 में लेने पर,
बनने वाली सरल रेखाओं की संख्या =4C2=4!2!2!=6
किन्तु 4 संरेखीय बिंदु, एक ही सरल रेखा बनायेंगे।
∴कुल वांछित सरल रेखाओं की संख्या =45−6+1=40
(ii) 10 में से 3 बिंदुओं में बिंदुओं को एक - एक साथ लेने पर बनने वाले त्रिभुजों की संख्या
=10C3=10!3!×7!=120
4 बिंदुओं में से 3 लेकर बनने वाले त्रिभुजों की संख्या
=4C3=4
∴ चारों संरेखीय बिंदुओं में से लेने पर त्रिभुज नहीं बन सकता
इसलिए, वांछित त्रिभुजों की कुल संख्या =120−4=116
Topper's Solved these Questions
- क्रमचय तथा संचयBook:BALAJI PUBLICATIONChapter:क्रमचय तथा संचयExercise:अभ्यास प्रश्न 10.1
Explore 20 Videos
- क्रमचय तथा संचयBook:BALAJI PUBLICATIONChapter:क्रमचय तथा संचयExercise:अभ्यास प्रश्न 10.2
Explore 9 Videos
- अवकलनBook:BALAJI PUBLICATIONChapter:अवकलनExercise:स्वमूल्यांकन परिक्षण
Explore 15 Videos
- गणितीय आगमन का सिद्धांत Book:BALAJI PUBLICATIONChapter:गणितीय आगमन का सिद्धांत Exercise:विवेचनात्मक सोच वाले प्रश्न
Explore 2 Videos
Similar Questions
कितने प्रकार से एक परीक्षार्थी सत्य/असत्य प्रकार के 10 प्रश्नों के उत्तर दे सकता है ?
View Solutionनिम्नलिखित का मान ज्ञात कीजिए -
(i) 30!28!, (ii) 11!−10!9!,
(iii) L.C.M. (6!,7!,8!)
View Solutionसिद्ध कीजिएः की महत्तम पूर्णांक फलन f(x)=[x],0<x<3,x=1 तथा x=2 पर अवलंकन नहीं है
View Solutionसिद्ध कीजिये की a+ar+ar2+...+aran−1=a(rn−1)r−1,r>1
View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
View Solutionसिद्ध कीजिए कि तीन बिन्दुओं, जिनके स्थिति सदिश ¯a,¯b,¯c हैं, को अन्तर्विष्ट करने वाले समतल पर अभिलम्ब ¯bׯc+¯cׯa+¯aׯb की दिशा में स्थित है |
View Solutionवक्र y=√7x+2−3 पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखा की प्रवणता 7 है।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionउस सरल रेखा का समीकरण, जो बिन्दुओं (-4, 6) तथा (8, 8) को मिलाने वाली रेखाखण्ड की लम्ब समद्विभाजक है, है
View Solutionउन बिन्दुओं को मिलाने वाली जीवा की लम्बाई, जिन पर सरल रेखा x3+y4=1 , वृत्त x2+y2=16925 को काटती है, है
View Solutionपरवलय y2=4ax की, उन जीवाओं के मध्य बिन्दुओं का बिन्दुपथ जो मूल बिन्दु से होकर जाती हैं, होगा
View Solutionपरवलय y2=6x के उन बिन्दुओं को जिनकी भुज 24 है, शीर्ष से मिलाने वाली रेखाओं का समीकरण है
View Solutionखण्ड 'अ'खण्ड 'ब'1.वृत्त के अन्तः बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(a)समकोण2.वृत्त के किसी बिंदु से खींची गयी स्पर्श रेखाओं की संख्या(b)स्पर्श रेखा3.वृत्त के बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखाओं की संख्या(c)शून्य4.स्पर्श रेखा और स्पर्श बिंदु से जाने वाली त्रिज्या के बीच बना कोण(d)एक5.वृत्त को केवल एक बिंदु पर प्रतिच्छेद करने वाली रेखा(e)दो
View Solutionनिम्नलिखित संख्या युग्मों को कार्तीय तल के बिन्दुओं के रूप में आलेखित कीजिए :
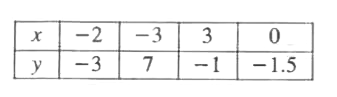
View Solutionउस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (3, 7) और (−1,−5) को मिलाने वाली रेखा को 2:3 के अनुपात में अन्तः विभाजित करता है।
View Solutionउस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (3, 7) और (−1,−5) को मिलाने वाली रेखा को 2:3 के अनुपात में अन्तः विभाजित करता है।
View Solution