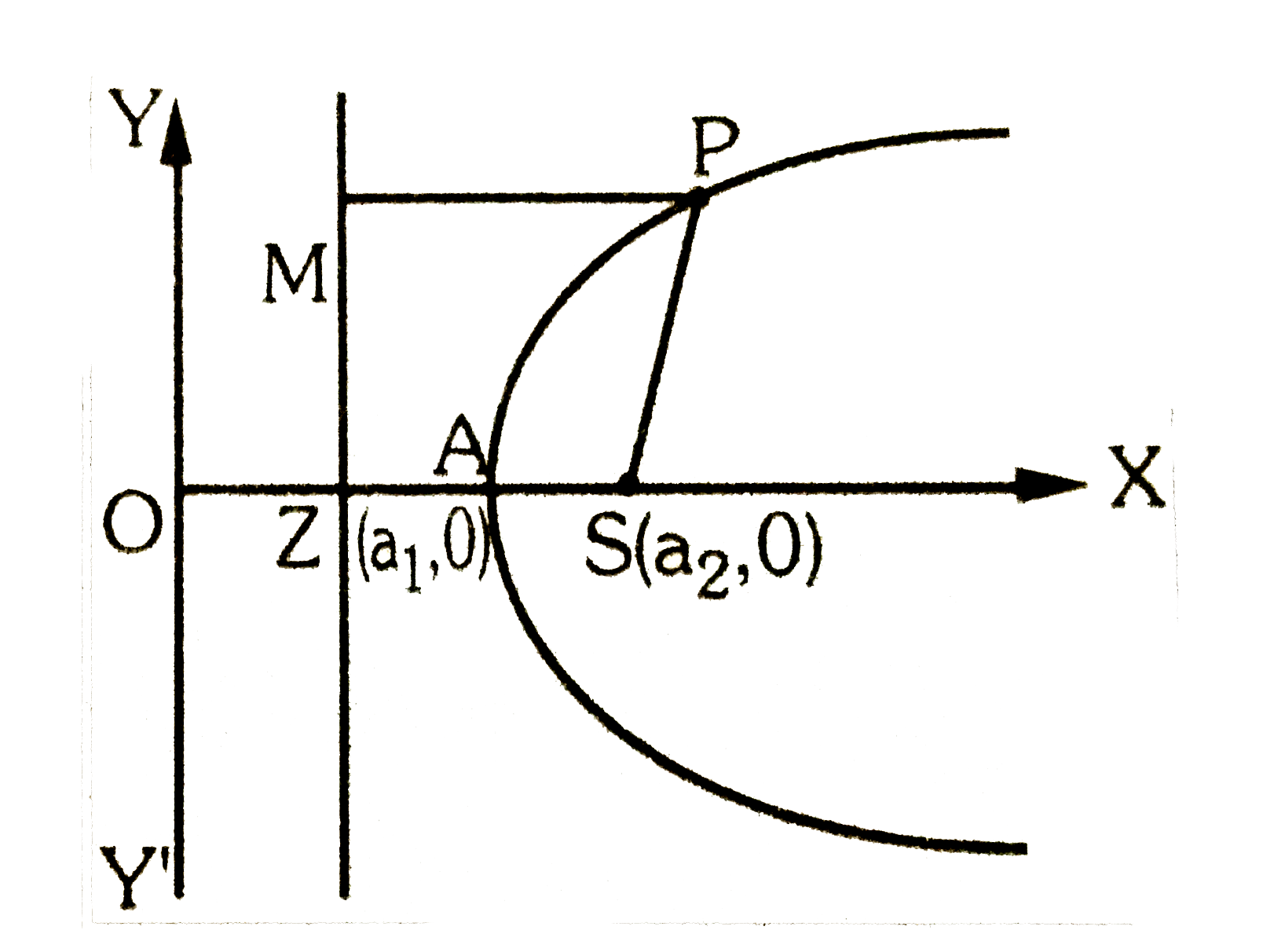
सिद्ध कीजिए कि उस परवलय का समीकरण जिसका शीर्ष और नाभि, मूल बिन्दु से क्रमशः a1 व a2 दूरियों पर हैं, यह है y2=4(a2−a1)(x−a1)
माना परवलय का शीर्ष A व नाभि S है।
तब
OA=a1,OS=a2
⇒ AS=OS−OA
=a2−a1
⇒ शीर्ष A के निर्देशांक =(a1,0)
तथा नाभि के निर्देशांक=(a2,0)
अब, माना AS परवलय का अक्ष है, जिसका समीकरण = 0 है।
यहाँ SA=AZ=a2−a1
⇒ OZ=OA−ZA
=a1−(a2−a1)
=2a1−a2
अब Z से होकर रेखा ZM खींचे यह रेखा परवलय के अक्ष पर लम्ब है तो ZM परवलय की नियता होगी और इस नियता का समीकरण x=2a1−a2
⇒ x−2a1+a2=0
माना इस परवलय पर कोई बिन्दु P =P (x, y ) है।
यदि P से नियता पर PM लम्ब है तब परिभाषानुसार,
PS=PM
⇒ √(x−a2)2+(y−0)2=x−2a1−a2
⇒ (x−a2)2+y2=(x−2a1+a2)2
⇒ y2=(x−2a1+a2)2−(x−a2)2
⇒ y2=4(a2−a1)(x−a1) यही परवलय का अभीष्ट समीकरण है।
Topper's Solved these Questions
- शंकु परिच्छेद : परवलय BOOK - BALAJI PUBLICATIONCHAPTER - शंकु परिच्छेद : परवलय EXERCISE - अभ्यास प्रश्न 16.1
30 Videos
- शंकु परिच्छेद : परवलय BOOK - BALAJI PUBLICATIONCHAPTER - शंकु परिच्छेद : परवलय EXERCISE - अभ्यास प्रश्न 16.2
1 Videos
- रैखिक असमिकाएँ BOOK - BALAJI PUBLICATIONCHAPTER - रैखिक असमिकाएँ EXERCISE - स्वमूल्यांकन परीक्षण ((B) विवेचनात्मक सोच वाले प्रश्न)
13 Videos
- शंकु परच्छेद: दीर्घवृत्तBOOK - BALAJI PUBLICATIONCHAPTER - शंकु परच्छेद: दीर्घवृत्तEXERCISE - स्वमूल्यांकन परीक्षण
19 Videos
Similar Questions
परवलय की समीकरण ज्ञात करो जिसका -
शीर्ष (0, 0) तथा नाभि (0,3) हो |
View Solutionसिध्द कीजिए की समीकरण y=ax2+bx+c, एक परवलय को निर्दशित करता है , जिसका अक्ष , y - अक्ष के समान्तर है |
View Solutionनिम्नलिखित प्रत्येक असमिका को हल कीजिए -
(i) 4x+3<5x+7
(ii) 3x−7>5x−1
View Solutionदीर्घवृत्त x225+y29=1 के नाभियो और शीर्षो के निर्देशांक, दीर्घ एवं लघु अक्ष की लम्बाईयाँ, उत्केन्द्रता और नाभिलम्ब जीवा की लम्बाई ज्ञात कीजिए |
View SolutionIf 0<a1<a2<....<an, then prove that tan−1(a1x−yx+a1y)+tan−1(a2−a11+a2a1)+tan−1(a3−a21+a3a2)+.......+tan−1(an−an−11+anan−1)+tan−1(1an)=tan−1(xy).
View Solutionprove that (1)/((a-a_(1))^(2)),(1)/(a-a_(1)),(1)/(a_(1))(1)/((a-a_(2))^(2)),(1)/(a-a_(2)),(1)/(a_(2))(1)/((a-a_(3))^(2)),(1)/(a-a_(3)),(1)/(a_(3))]|=(-a^(2)(a_(1)-a_(2))(a_(2)-a_(3))(a_(3)-a_(1)))/(a_(1)a_(2)a_(3)(a-a_(1))^(2)(a-a_(2))^(2)(a-a_(3))^(2))
View SolutionIf a_(1),a_(2)...a_(n) are the first n terms of an Ap with a_(1)=0 and d!=0 then (a_(3)-a_(2))/(a_(2))+(a_(4)-a_(2))/(a_(3))+(a_(5)-a_(2))/(a_(4))...+(a_(n)-a_(2))/(a_(n-1)) is
View SolutionIf (1+x)2n=a0+a1x+a2x2+…+a2nx2n, then
(a0−a2+a4−a6+…−a2n)2+(a1−a3+a5−a7+...+a2n−1)2 is equal to
View Solutiona1,a2,a3.....an are in H.P. a1a2+a3+...+an,a2a1+a3+...+an,a3a1+a2+a4+...+an,...,ana1+a2+...+an−1 are in
View SolutionIf a2a3a1a4=a2+a3a1+a4=3(a2−a3a1−a4), then a1,a2,a3,a4 are in
View Solutionif a1,a2,a+3……,a12 are in A.P and
Δ1=∣∣ ∣∣a1a5a1a2a2a6a2a3a3a7a3a4∣∣ ∣∣Δ3=∣∣ ∣∣a2b10a2a3a3a11a3a4a3a12a4a5∣∣ ∣∣
then Δ2:Δ2=_____
View SolutionIf a1,a2,a3,a4,a5 are in HP, then a1a2+a2a3+a3a4+a4a5 is eqiual to
View SolutionIf a1,a2,a3,a4,,……,an−1,an are distinct non-zero real numbers such that (a21+a22+a23+…..+a2n−1)x2+2(a1a2+a2a3+a3a4+……+an−1an)x+(a22+a23+a24+......+a2n)≤0 then a1,a2,a3,.....,an−1,an are in
View SolutionIf ∣∣ ∣∣1+a1a2a3a11+a2a3a1a21+a3∣∣ ∣∣=0 then a1+a2+a3=
View SolutionIf the coefficients of the consicutive four terms in the expansion of (1+x)n be a1,a2,a3anda4 respectively , show that ,
a1a1+a2+a3a3+a4=2.a2a2+a3.
View SolutionIf a2a3a1a4=a2+a3a1+a4=3(a2−a3a1−a4) , then :
a1,a2,a3,a4 are in :
View Solution
