बिंदुओं P,Q,R,S के निर्देशांक क्रमशः (4,7,8), (-1,-2,1) , (2,3,4) तक (1,2,5) हैं । सिद्ध कीजिए कि PQ तथा RS प्रतिच्छेद करते हैं तथा प्रतिच्छेदन बिंदु भी ज्ञात कीजिए ।
माना रेखाएँ PQ तथा RS एक - दूसरे को बिंदु A पर प्रतिच्छेद करती हैं ।
यदि A,PQ को λ1:1 के अनुपात में अन्तः विभाजित करता हैं तब
A ≡(−λ1λ1+1,−2λ1+7λ1+1,λ1+8λ1+1) ....(i)
अब माना A, रेखाखण्ड RS को λ2:1 के अनुपात में विभाजित करता हैं ।
तब A=(λ2+2λ2+1) ....(ii)
समीकरण (i) व (ii) से
λ1+4λ1+1=λ2+2λ2+1,−2λ1+7λ1+1=2λ2+3λ2+1
तथा λ1+8λ1+1=5λ2+4λ2+1
उपरोक्त समीकरण को हल करने पर
λ1=λ2
तथा 2λ21+3λ1−3λ1−2=0
⇒λ1=±1=λ2
यहाँ λ1=λ2≠−1 सम्भव नहीं हैं क्योंकि इस स्थिति में रेखाखण्ड एक - दूसरे के समान्तर होंगे ।
इसलिए λ1=λ2=1
⇒ A के निर्देशांक = (−1+42,−2+72,1+82)
=(32,52,92)

Topper's Solved these Questions
- त्रिविमीय ज्यामिति का परिचय BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति का परिचय EXERCISE - अभ्यास प्रश्न 19.1
12 Videos
- त्रिविमीय ज्यामिति का परिचय BOOK - BALAJI PUBLICATIONCHAPTER - त्रिविमीय ज्यामिति का परिचय EXERCISE - अभ्यास प्रश्न 19.2
21 Videos
- त्रिकोणमितीय समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिकोणमितीय समीकरण EXERCISE - स्वमूल्यांकन परीक्षण
13 Videos
- द्विघात समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - द्विघात समीकरण EXERCISE - स्वमूल्यांकन परीक्षण ( विवेचनात्मक सोच वाले प्रश्न )
7 Videos
Similar Questions
उन अष्टांशों के नाम लिखिये जिनमें (4,-2,-3) बिंदु स्थित हैं ।
View Solutionबिंदुओं (4,3,7) व (1,-1,-5) के बीच की दूरी ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि - secθ−1=(√2−1)⋅tanθ का हल θ=2nπ होगा ।
View Solutionx2−(3√2−2i)x−6i√2=0
View SolutionIf the points P,Q,R,S are (4,7,8),(-1,-2,1),(2,3,4) and (1,2,5) respectively show that PQ and RS intersect. Also find the point of intersection.
View Solutionयदि बिंदु P,Q,R तथा S क्रमश: (4,7,8) , (-1,-2,1), (2,3,4) तथा (1,2,5) हैं, सिद्ध कीजिए की PQ तथा RS परस्पर प्रतिछेदित होते हैं| प्रतिच्छेद बिंदु भी ज्ञात कीजिए|
View Solutionबिंदु (4,7,8), (2,3,4),(-1,-2,1) तथा (1,2,5) शीर्ष है:
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए , जो रेखाओ x+y=3 तथा 2x+3y=7 के प्रतिच्छेद बिंदु को रेखाओ 2x+3y=8 तथा 3x−y=1 के प्रतिच्छेद बिंदु से मिलती है ।
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionदिए गये आकृति से बिन्दुओ P, Q, R व S के निर्देशांक ज्ञात कीजिए -
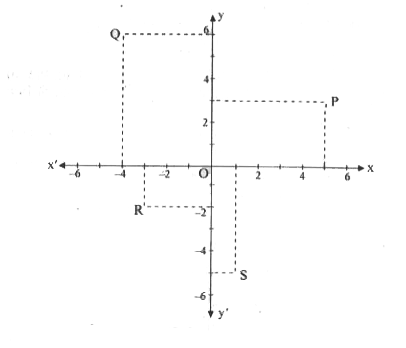
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View Solutionयदि O मूलबिंदु तथा बिंदु P के निर्देशांक (3,-4) हों तो सदिश ¯¯¯¯¯¯OP को एकांक सदिशों ¯i तथा ¯j के पदों में व्यक्त कीजिए तथा ∣∣¯¯¯¯¯¯OP∣∣ भी ज्ञात कीजिए।
View Solutionबिंदुओं P और Q के निर्देशांक निम्नानुसार है:
P(5,−7),Q(−3,2)
प्रत्येक स्थिति में सदिश ¯¯¯¯¯¯PQ को एकांक सदिशों ¯i और ¯j के पदों में व्यक्त कीजिए तथा ∣∣¯¯¯¯¯¯PQ∣∣ की गणना कीजिए।
View Solutionयदि P और Q के स्थिति सदिश क्रमशः 3¯i+5¯j−7¯k तथा 3¯i−4¯j+¯k हों तो ∣∣¯¯¯¯¯¯PQ∣∣ ज्ञात कीजिए तथा ¯¯¯¯¯¯PQ की दिशा में एकांक सदिश ज्ञात कीजिए।
View Solution
