एकसमान चुंबकीय क्षेत्र में स्वतंत्रतापूर्वक लटकी धारावाही आयताकार कुंडली पर लगने वाले बलयुग्म का सूत्र स्थापित कीजिए ।किस दशा में बलयुग्म (i) अधिकतम (ii) न्यूनतम होगा ?
जब किसी एकसमान चुंबकीय क्षेत्र में स्वतंत्रतापूर्वक लटकी किसी कुंडली में विधुत धारा प्रवाहित की जाती है , तो कुंडली पर एक बलयुग्म आरोपित होता है , जो कुंडली को घुमाकर उसके तल को चुंबकीय क्षेत्र के लंबवत करने का प्रयास करता है ।
(a)चित्र के अनुसार , माना कि ABCD एक आयताकार कुंडली है , जिसकी भुजा AB=CD=l तथा AD=BC=bहै ।
इसे एकसमान चुंबकीय क्षेत्र B में रखा जाता है ।
कुंडली में धारा I प्रवाहित कि जाती है । कुंडली की भुजाएँ AB तथा CD चुंबकीय क्षेत्र के लंबवत है , अतः इन भुजाओं पर BIl बल विपरीत दिशा में लगेंगे , जिससे एक बलयुग्म कुंडली पर लगता है । जबकि भुजा BC तथा AD चुंबकीय क्षेत्र के समांतर है ।
अतः इन भुजाओं पर कोई बल कार्य नहीं करता । इस प्रकार कुंडली की भुजा AB और CD पर लगने वाले बल बलयुग्म को विक्षेपक बलयुग्म कहते है ।
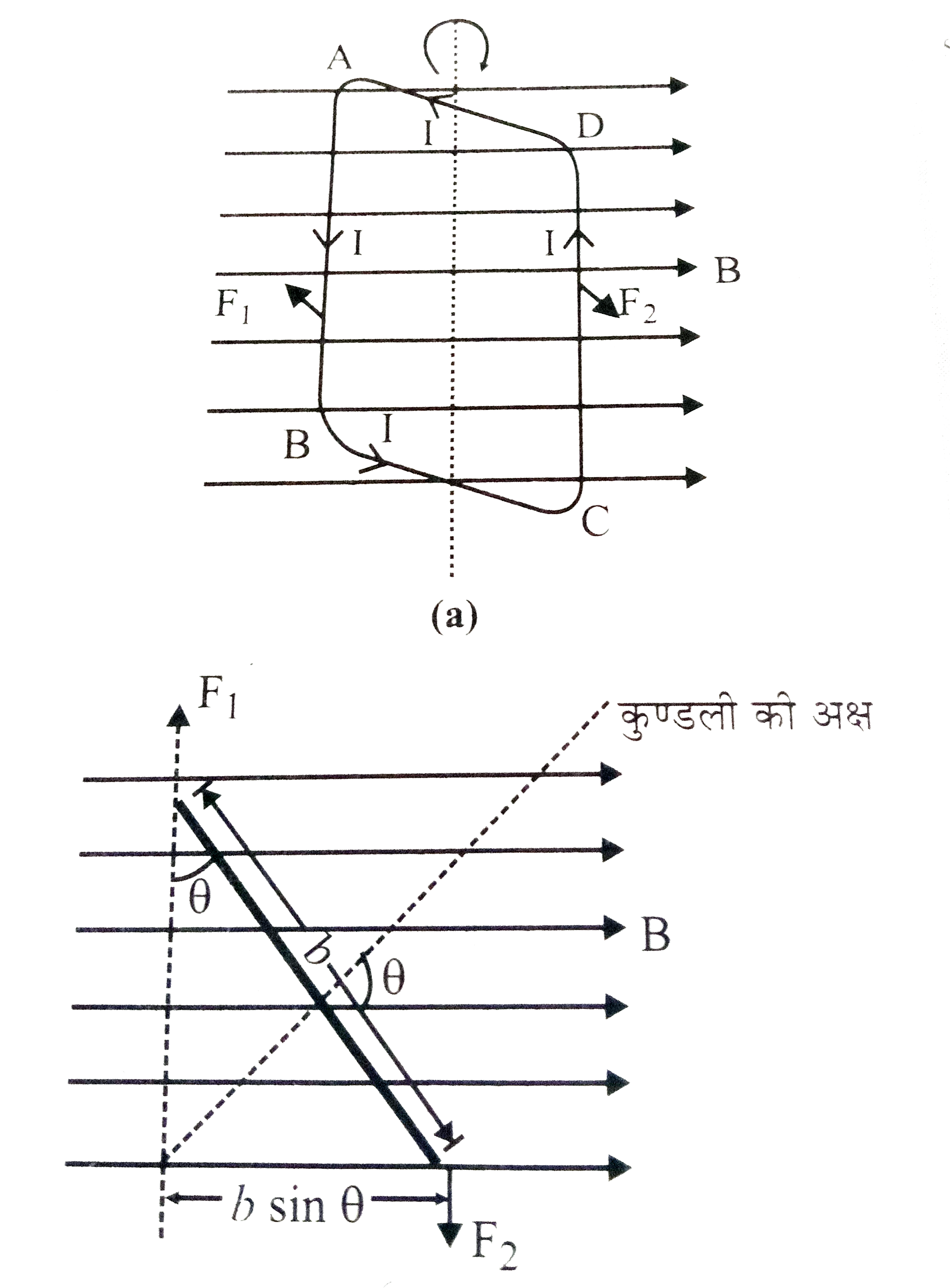
यदि किसी क्षण चित्र (b) के अनुसार कुंडली का अक्ष चुंबकीय क्षेत्र से θकोण बनाता है , तो दोनों बल F1एवं F2( दोनों का परिमाण BIl) के बीच की लंबवत दूरी bsinθ होगी ।
अतः विक्षेपक बलयुग्म का आघूर्ण
τ= बल × दोनों बलों के बीच लंबवत दूरी
=BIl×bsinθ=BIl⋅bsinθ
=BIAsinθ ...(1)
जहाँ A=lb,कुंडली के लूप का क्षेत्रफल है । अब यदि कुंडली में फेरों की संख्या n हो , तो विक्षेपक बलयुग्म का आघूर्ण
τ=nIABsinθ ...(2)
यदि एक समान चुंबकीय क्षेत्र में धारावाही कुंडली पर लगने वाले बल आघूर्ण का सूत्र है । यह आघूर्ण कुंडली को घुमाकर चुंबकीय क्षेत्र के लंबवत अर्थात कुंडली के अक्ष को चुंबकीय क्षेत्र के समांतर लाने का प्रयास करता है । सदिश रूप में समीकरण (2) को निम्नानुसार लिखा जा सकता है -
→τ=I(→A×→B) ...(3)
स्थिति 1.यदि θ=90∘ हो - इस स्थिति में sinθ=sin90∘=1,अतः समीकरण (2) से ,
Z=nIAB = अधिकतम
अर्थात जब धारा लूप या कुंडली का तल चुंबकीय क्षेत्र के समांतर होता है , तो उस पर लगने वाला बल आघूर्ण अधिकतम होता है ।
स्थिति 2. यदि θ=0∘ हो - इस स्थिति में
sinθ=sin0∘=0
अतः समीकरण (2) से ,
τ=nIAB×0=0
अर्थात जब धारा लूप या कुंडली का तल चुंबकीय क्षेत्र के लंबवत होता है , तो उस पर लगने वाला बल आघूर्ण का मान शून्य होता है ।
Topper's Solved these Questions
- गतिमान आवेश ओर चुम्बकत्व BOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश ओर चुम्बकत्व EXERCISE - दीर्घ उत्तरीय प्रश्न
6 Videos
- गतिमान आवेश ओर चुम्बकत्व BOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश ओर चुम्बकत्व EXERCISE - आंकिक प्रश्न
12 Videos
- गतिमान आवेश ओर चुम्बकत्व BOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश ओर चुम्बकत्व EXERCISE - आंकिक प्रश्न
12 Videos
- किरण प्रकाशिकी एवं प्रकाशीय यंत्र BOOK - PRABODH PUBLICATIONCHAPTER - किरण प्रकाशिकी एवं प्रकाशीय यंत्र EXERCISE - आंकिक प्रश्न
12 Videos
- गतिमान आवेश और चुंबकत्वBOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश और चुंबकत्वEXERCISE - मूल्य आधारित प्रश्न
3 Videos
Similar Questions
किस वृत्ताकार धारावाही कुंडली कि अक्ष पर स्थित किसी बिंदु पर चुम्बकीय क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए ।
View Solutionतार की एक वृत्ताकार कुण्डली में 100 फेरे हैं । प्रत्येक की त्रिज्या 8.0 cm है ओर इनमें 0.40 A विद्युत धारा प्रवाहित हो रही है । कुण्डली हो रही है । कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का परिणाम क्या होगा ?
View Solutionतार की एक वृत्ताकार कुण्डली में 100 फेरे हैं । प्रत्येक की त्रिज्या 8.0 cm है ओर इनमें 0.40 A विद्युत धारा प्रवाहित हो रही है । कुण्डली हो रही है । कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का परिणाम क्या होगा ?
View Solutionएक मोमबत्ती को अवतल दर्पण के सम्मुख 4 सेमी की दुरी पर रखा गया है । दर्पण की वक्रता त्रिज्या 10 सेमी है। प्रतिबिम्ब की स्थिति, प्रकृति आवर्धन क्षमता परिकलित कीजिए।
View Solutionदो समांतर रेखीय धारावाही चालक में धारा समान दिशा में प्रवाहित होने पर वे एक - दूसरे को आकर्षित करते है तथा धारा विपरीत दिशा में प्रवाहित होने पर वे एक - दूसरे को प्रतिकर्षित करते है । दो समांतर चालकों के मध्य की दूरी r है इनमें धारा I1 व I2के कारण निर्वात में प्रति एकांक लम्बाई पर क्रियाशील बल का मान F=μ04π2I1I2r
है । उपरोक्त अनुच्छेद को पढ़कर निम्न प्रश्नों के उत्तर दीजिए -
(i) दोनों रेखीय समांतर धारावाही चालकों के मध्य बल का कारण क्या है ?
(ii) यदि चालक तारों की लम्बाई 2 सेमी. तथा 20 सेमी. हो उनमें प्रवाहित धारा 2A व 5A हो । वे एक - दूसरे से 4 सेमी. की दूरी पर है । 20 cm लम्बे तार पर बल का मान क्या होगा ।
(iii) इसके अध्ययन की दैनिक जीवन में क्या उपयोगिता है ?
View Solutionएकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionचुंबकीय क्षेत्र में किसी विद्युत धारावाही चालक पर बल
View Solutionविद्युत धारावाही चालक पर चुंबकीय बल | दो समांतर विद्युत धाराओं के बीच बल-ऐम्पियर | एकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
View Solutionधारावाही चालक को चुंबकीय क्षेत्र में रखने पर लगने वाला बल |UP बोर्ड SPECIAL
View Solutionधारावाही वृत्ताकार लूप और कुंडली के अक्ष पर चुंबकीय क्षेत्र
View Solutionधारावाही तार पर एकसमान चुंबकीय क्षेत्र मे लगने वाला बल
View Solutionएकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण चल कुंडली धारामापी
View Solutionएकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionचुंबकीय क्षेत्र में धारावाही चालक तार पर बल
View Solutionधारावाही तारों में चुंबकीय क्षेत्र | विभिन्न मामले
View Solution