जांच कीजिये कि कोष्टकों मि दिए हुए मान, दिए संगत समीकरणों के हल हैं या नहीं:
a) n+5=19(n=1)
b) 7n+5=19(n=−2), c) 7n+5=19(n=2), d) 4p−3=13(p=1), e) 4p−3=13(p=−4), f) 4p−3=13(p=0)
The correct Answer is:(a) नहीं (b) नहीं (c) हाँ (d) नहीं (e) नहीं f) नहीं
Step by step video, text & image solution for जांच कीजिये कि कोष्टकों मि दिए हुए मान, दिए संगत समीकरणों के हल हैं या नहीं: a) n+5=19(n=1) b) 7n+5=19(n=-2), c) 7n+5=19(n=2), d) 4p-3=13(p=1), e) 4p-3=13(p=-4), f) 4p-3=13(p=0) by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- सरल समीकरण Book:NCERT HINDIChapter:सरल समीकरण Exercise:प्रशनावली 4.2
Explore 5 Videos
- सरल समीकरण Book:NCERT HINDIChapter:सरल समीकरण Exercise:प्रशनावली 4.3
Explore 4 Videos
- सरल समीकरण Book:NCERT HINDIChapter:सरल समीकरण Exercise:प्रयास कीजिये
Explore 6 Videos
- सममिति Book:NCERT HINDIChapter:सममिति Exercise:इन्हें कीजिए
Explore 1 Video
Similar Questions
पहले चर को पृथक करने वाला चरण बताइये और फिर समीकरण को हल कीजिये:
a) x−1=0, b) x+1=0, c) x−1=5, d) x+6=2
View Solutionनिम्नलिखित समीकरणों को हल कीजिये:
(a) 2y+52=372, (b) 5t+28=10, (c) a5+3=2, (d) q4+7=5
View Solutionव्यंजक (10y-20) का मान y के मान पर निर्भर करता है। y को पांच भिन्न-भिन्न मान देकर तथा y के प्रत्येक मान के लिए (10y-20) का मान ज्ञात इसकी पृष्टि कीजिये। (10y-20) के प्राप्त किये गए विभिंन मनो से, क्या आप (10y−20)=50 का कोई हल देख रहे है? यदि कोई गाल प्राप्त नहीं हुआ है, तो y को कुछ अन्य मान देकर, ज्ञात कीजिये की प्रतिबन्ध 10y−20=50 संतुष्ट होता है या नहीं।
View Solutionअंग्रेजी वर्णमाला के कुछ अक्षरों में अद्भुत एवं आकर्षक सममितीय संरचनाएं है। किन बड़े अक्षरों में केवल एक ही सममित रेखा है किन बड़े अक्षरों में क्रम 2 की घूर्णन सममिति हैं
उपरोक्त प्रकार से सोचते हुए आप निम्नलिखित सारणी की भरने में समर्थ हो पाएंगें:
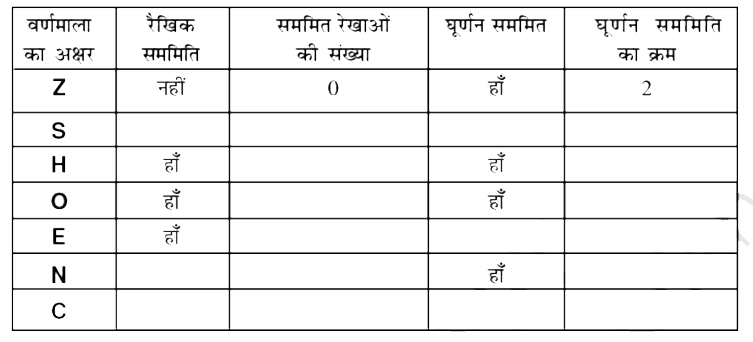
View SolutionCheck whether the value given in the brackets is a solution to the given equation or not: (a) n+5=19(n=1) (b) 7n+5=19(n=−2) (c) 7n+5=19(n=2) (d) 4p−3=13(p=1) (e) 4p−3=13(p=4) (f) 4p−3=13(p=0)
View Solution(1625−12115)÷3481=? (a) 1919 (b) 1913 (c) 2813 (d) 3219 (e) None of these
View SolutionThe value of 2n−1−2n2n+4+2n+1 is a. −136 b. 23 c. 113 d. 513
View SolutionIf A={p∈N,p is a prime and p=7n2+3n+3n for some n∈N), then the number of elements in the set A is
View SolutionIf {p∈N:p is a primeandp=7n2+3n+3nfor some n∈N}' then the number of elements in the set A, is
View SolutionIf the coefficients of the pth , (p+1)and(p+2) terms in the expansions of (1+x)n are in A.P , show that , n2−n(4p+1)+4p2−2=0
View Solution4P(X = 4) = P(X = 2) மற்றும் n = 6 எனும்படி உள்ள X~B(n,p)-ன் பரவலின், சராசரி மற்றும் திட்டவிலக்கம் ஆகியவற்றைக் காண்க.
View SolutionCheck whether the value given in the brackets is a solution to the given equation or not: (a) n+5=19(n=1) (b) 7n+5=19(n=−2) (c) 7n+5=19(n=2) (d) 4p−3=13(p=1) (e) 4p−3=13(p=4) (f) 4p−3=13(p=0)
View SolutionIf P(n,5):P(n,3)=2:1 find n
View SolutionLet P(n)=23n−7n−1 then P(n) is divisible by
View SolutionLet P(n)=n55+n33+7n15 is natural number , is true statement
View Solution
