आइए अब हम निम्नलिखित बारंबारता बंटन सारणी लें, जिसमे एक कक्षा के 38 विद्यार्थियों के भर दिए गए हैः
अब, यदि 35.5 kg और 40.5 kg के भार वाले दो और विद्यार्थी इस कक्षा में आ जाएँ तो उन्हें किस वर्ग अंतराल में रखा जाएगा? उन्हें न तो हम उन अंतरालों में रख सकते हैं जिनकी अंतिम संख्या 35 या 40 हैं और न ही इन्हें हम उन अंतरालों में रख सकते हैं जो इनके बाद आते हैं । ऐसा इसलिए है, क्योंकि दो क्रमागत वर्गों (consecutive classes) की उपरि और निम्न सीमाओं के बीच रिक्त स्थान है । अतः इस स्थिति में हमें अंतरालों को विभक्त करना होता है, जिससे की क्रमागत अंतरालों की उपरि और निम्न सीमाएँ समान हो जाएँ । इसके लिए हमें एक वर्ग की उपरि सीमा और उसके बाद के वर्ग की निम्न सीमा के बीच का अंतर ज्ञात करना होता है । तब हम इस अंतर के आधे भाग को प्रत्येक उपरि सीमा में जोड़ देते हैं और बीच इसी राशि को प्रत्येक निम्न सीमा में से घटा देते हैं ।
उदाहरण की लिए, वर्ग 31-35 और 36-40 लीजिए ।
36-40 की निम्न सीमा = 36
31-35 की उपरि सीमा = 35
अंतर = 36-35 = 1
अन्तः, अंतर का आधा =12=0.5
इस प्रकार, वर्ग 31-35 से बना नया वर्ग अंतराल (31-0.5) - (35+0.5) = 30.05 - 35.5 है । इसी प्रकार, 36-40 से बना नया वर्ग अंतराल
= (36-0.5) - (40 + 0.5)
= 35.5 - 40.5
इस प्रक्रिया को आगे बढ़ाने पर निम्नलिखित संतत वर्ग (continuous classes) प्राप्त होते हैं: 30.5-35.5, 35.5-40.5, 40.5-45.5, 45.5-50.5 50.5-55.5, 55.5-60, 60.5-65.5, 65.-70.5, 70.5-75.5
अब हम इन वर्गों में नए विधार्थियों के भार सम्मिलित कर सकते हैं । परन्तु, ऐसा करने से एक और समस्या आती है । वह यह है की 35.5 दोनों ही वर्गों 30.5-35.5 और और 35.5-40.5 में है । वह यह है की आपके विचार से इस भार को किस वर्ग में रखना चिहिए ?
यदि ऐसे दोनों वर्गों में रखा जाए, तो इसकी गिनती दो बार करनी होगी ।
अतः परंपरा के अनुसार, हम 35.5 को वर्ग 35.5-40.5 में रखते हैं न की वर्ग 30.5-35.5 में, इसी प्रकार, 40.5 को वर्ग 40.5-45.5 में रखा जाता है न की वर्ग 35.5-40.5 में ।
अतः नए भार 35.5 kg और 40.5 kg को क्रमशः 35.5-40.5 और 40.5-45.5 में सम्मिलित किया जाएगा । अब इन कल्पनाओं को ध्यान में रखने पर एक नई बारंबारता बंटन सारणी प्राप्त होगी, जैसा की नीचे दिखाई गई हैः
आइए अब हम क्रियाकलाप 1 में आपके द्वारा एकत्रित किए गए आकंड़ों को लें । इस बार हम चाहेंगे की आप इन आकंड़ों को एक बारंबारता बंटन सारणी की रूप में प्रस्तुत करें ।
Step by step video & image solution for आइए अब हम निम्नलिखित बारंबारता बंटन सारणी लें, जिसमे एक कक्षा के 38 विद्यार्थियों के भर दिए गए हैः अब, यदि 35.5 kg और 40.5 kg के भार वाले दो और विद्यार्थी इस कक्षा में आ जाएँ तो उन्हें किस वर्ग अंतराल में रखा जाएगा? उन्हें न तो हम उन अंतरालों में रख सकते हैं जिनकी अंतिम संख्या 35 या 40 हैं और न ही इन्हें हम उन अंतरालों में रख सकते हैं जो इनके बाद आते हैं । ऐसा इसलिए है, क्योंकि दो क्रमागत वर्गों (consecutive classes) की उपरि और निम्न सीमाओं के बीच रिक्त स्थान है । अतः इस स्थिति में हमें अंतरालों को विभक्त करना होता है, जिससे की क्रमागत अंतरालों की उपरि और निम्न सीमाएँ समान हो जाएँ । इसके लिए हमें एक वर्ग की उपरि सीमा और उसके बाद के वर्ग की निम्न सीमा के बीच का अंतर ज्ञात करना होता है । तब हम इस अंतर के आधे भाग को प्रत्येक उपरि सीमा में जोड़ देते हैं और बीच इसी राशि को प्रत्येक निम्न सीमा में से घटा देते हैं । उदाहरण की लिए, वर्ग 31-35 और 36-40 लीजिए । 36-40 की निम्न सीमा = 36 31-35 की उपरि सीमा = 35 अंतर = 36-35 = 1 अन्तः, अंतर का आधा =(1)/(2) = 0.5 इस प्रकार, वर्ग 31-35 से बना नया वर्ग अंतराल (31-0.5) - (35+0.5) = 30.05 - 35.5 है । इसी प्रकार, 36-40 से बना नया वर्ग अंतराल = (36-0.5) - (40 + 0.5) = 35.5 - 40.5 इस प्रक्रिया को आगे बढ़ाने पर निम्नलिखित संतत वर्ग (continuous classes) प्राप्त होते हैं: 30.5-35.5, 35.5-40.5, 40.5-45.5, 45.5-50.5 50.5-55.5, 55.5-60, 60.5-65.5, 65.-70.5, 70.5-75.5 अब हम इन वर्गों में नए विधार्थियों के भार सम्मिलित कर सकते हैं । परन्तु, ऐसा करने से एक और समस्या आती है । वह यह है की 35.5 दोनों ही वर्गों 30.5-35.5 और और 35.5-40.5 में है । वह यह है की आपके विचार से इस भार को किस वर्ग में रखना चिहिए ? यदि ऐसे दोनों वर्गों में रखा जाए, तो इसकी गिनती दो बार करनी होगी । अतः परंपरा के अनुसार, हम 35.5 को वर्ग 35.5-40.5 में रखते हैं न की वर्ग 30.5-35.5 में, इसी प्रकार, 40.5 को वर्ग 40.5-45.5 में रखा जाता है न की वर्ग 35.5-40.5 में । अतः नए भार 35.5 kg और 40.5 kg को क्रमशः 35.5-40.5 और 40.5-45.5 में सम्मिलित किया जाएगा । अब इन कल्पनाओं को ध्यान में रखने पर एक नई बारंबारता बंटन सारणी प्राप्त होगी, जैसा की नीचे दिखाई गई हैः आइए अब हम क्रियाकलाप 1 में आपके द्वारा एकत्रित किए गए आकंड़ों को लें । इस बार हम चाहेंगे की आप इन आकंड़ों को एक बारंबारता बंटन सारणी की रूप में प्रस्तुत करें । by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - NCERT HINDICHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.12videos
सांख्यिकी
- BOOK - NCERT HINDICHAPTER - सांख्यिकीEXERCISE - प्रश्नावली 14.29videos
सांख्यिकी
- BOOK - NCERT HINDICHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.48videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NCERT HINDICHAPTER - हीरोन का सूत्र EXERCISE - प्रश्नावली 12.29videos
हीरोन का सूत्र
Similar Questions
उन आंकड़ों के पाँच उदाहरण दीजिए जिन्हे आप अपने दैनिक जीवन से एकत्रित कर सकते हैं।
05:41View Solutionआठवीं कक्षा के 30 विद्यार्थियों के रक्त समूह ये हैः
A,B,O,O,AB,O,A,O,B,A,O,B,A,O,OA,AB,O,A,A,O,O,AB,B,A,O,B,A,B,O
इन आंकड़ों को एक बारंबारता बंटन सारणी के रूप में प्रस्तुत कीजिए। बताइए की इन विद्यार्थियों में कौन-सा रक्त समूह अधिक सामान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है।03:07View Solutionसमांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है । दर्शाइए की समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है ।
02:10View Solutionएक पार्क चतुर्भुज ABCD के आकार का है, जिसमे ∠C=90∘,AB=9 मी, BC=12 मी, CD=5 मी और AD=8 मी है। इस पार्क का कितना क्षेत्रफल है?
06:22View SolutionMatch the following Column A to Column B
 View Solution
View Solutionयदि A और B समान कोटि के वर्ग आव्यूह हैं, तो निम्नलिखित में से कौन-सा सही है ?
View Solutionनिम्नलिखित में से कौन-सी संख्या 27 और 97 के मध्य में नहीं हैं :
View Solutionएक कक्षा के विद्यार्थियों के पंक्तियों में खड़ा होना है | यदि प्रत्येक पंक्ति में 1 विद्यार्थी अधिक होता हो तो 2 पंक्ति कम होती | यदि प्रत्येक पंक्ति में 1 विद्यार्थ कम होता तो 3 पंक्तियाँ अधिक बनती | कक्षा में विद्यार्थियों के संख्या ज्ञात करें |
02:37View Solutionनिम्नलिखित गद्यांश को ध्यानपूर्वक पढ़कर पूछे गए प्रश्नों के उत्तर लिखिए:
अकसर हम या तो गुजरे हुए दिनों की खट्टी-मीठी यादों में उलझे रहते हैं या भविष्य के रंगीन सपने देखते हैं। हम या तो भूतकाल में रहते हैं या भविष्यकाल । असल में दोनों काल मिथ्या हैं। एक चला गया है, दूसरा आया नहीं है। हमारे सामने जो वर्तमान क्षण है, वही सत्य है। उसी में जीना चाहिए।
गद्यांश में लेखक ने किन बातों में उलझे रहने की बात कही है?01:48View Solutionनिम्नलिखित गद्यांश को ध्यानपूर्वक पढ़कर पूछे गए प्रश्नों के उत्तर लिखिए: अकसर हम या तो गुजरे हुए दिनों की खट्टी-मीठी यादों में उलझे रहते हैं या भविष्य के रंगीन सपने देखते हैं। हम या तो भूतकाल में रहते हैं या भविष्यकाल । असल में दोनों काल मिथ्या हैं। एक चला गया है, दूसरा आया नहीं है। हमारे सामने जो वर्तमान क्षण है, वही सत्य है। उसी में जीना चाहिए। आशय स्पष्ट कीजिए : असल में दोनों काल मिथ्या हैं।
01:14View Solutionनिम्नलिखित गद्यांश को ध्यानपूर्वक पढ़कर पूछे गए प्रश्नों के उत्तर लिखिए:
अकसर हम या तो गुजरे हुए दिनों की खट्टी-मीठी यादों में उलझे रहते हैं या भविष्य के रंगीन सपने देखते हैं। हम या तो भूतकाल में रहते हैं या भविष्यकाल । असल में दोनों काल मिथ्या हैं। एक चला गया है, दूसरा आया नहीं है। हमारे सामने जो वर्तमान क्षण है, वही सत्य है। उसी में जीना चाहिए।
लेखक ने सत्य किसे कहा है और क्यों?View Solutionकिसी विद्यालय के शिक्षकों के भार किलोग्राम में नीचे दिए गए हैं। इन्हें बारंबारता सारणी में प्रकट कीजिए:
65,62,61, 65,62,70,62,70,75,72,70,60, 80,85,63,85,67,80,75,65.View Solutionवे शब्द जो धातु या शब्द के अंत में जोड़े जाते हैं उन्हें काया कहते हैं ?
01:57View SolutionIf two angles of a triangle are 21^(@) and 38^(@) , then the triangle is यदि त्रिभुज के दो कोण 21^(@) और 38^(@) हैं, तो त्रिभुज हैं
02:50View Solutionनीचे दिए गए चार तत्वों पर विचार कीजिए, जिन्हें आवर्त सारणी के दीर्घाकार रूप के अनुसार निरूपित किया गया है,
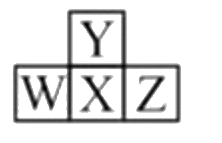
यहाँ W, Y और Z तत्व 'X' के संदर्भ में बाएं, ऊपर और दाएं उपस्थित हैं और तत्व 'X' सोलहवें वर्ग और तीसरे आवर्त से संबंधित हैं। तब दी गई सूचना के अनुसार दिए गए तत्वों के बारे में गलत कथन है :03:13View Solutionपरमाणु क्रमांक 20 वाले एक तत्व को आवर्त सारणी के किस आवर्त में रखा जाएगा?
View Solution

