दर्शाइए की a1,a2,...........,an..... से एक A.P. बनाती है,यदि an नीचे दिए अनुसार परिभाषित है:
(i)an=3+4n (ii)an=9−5n
साथ ही,प्रत्येक स्थिति में,प्रथम 15 पदों का योग ज्ञात कीजिए|
अनुक्रम का न वां पद an=3+4n
n=1 रखने पर a1=3+4×1=3+4=7
n=2 रखने पर a2=3+4×2=3+8=11
n=3 रखने पर a3=3+4×3=3+12=15
अब a2−a1=11−7=4
∵ a3−a2=15−11=4
∵ a2−a1=a3−a2=4
∴ अनुक्रम के दो क्रमागत पदों का अंतर् नियत है|
अतः अनुक्रम A.P.है|
अब d=4 तथा a =7
प्रथम 15 पदों का योग
=n2[2a+(n−1)d]
=152[2×7+(15−1)×4]
=152[14+56]=152×70=525 ltbr gt (ii)an=9−5n
n=1 रखने पर,a1=9−5×1=9−5=4
n=2 a2=9−5×2=9−10=−1
n=3 रखने पर a3=9−5×3=9−15=−6
अब a2−a1=−1−4=−5
a3−a2=−6−(−1)=−6+1=−5
∵ a2−a1=a3−a2=−5
∴ अनुक्रम के दो क्रमागत पदों का अंतर् नियत है| अतः अनुक्रम A.P. है
अब d =-5 ,a =4
∴ प्रथम 15 पदों का योग
=n2[2a+(n−1)d]
=152[2×4+(15−1)(−5)]
=152(8−70)=152×(−62)=−465
Topper's Solved these Questions
- समान्तर श्रेढ़ी BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - प्रश्नावली 5.4
5 Videos
- समान्तर श्रेढ़ी BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - विविध प्रश्नावली (अतिलघु उतरिए प्रश्न)
10 Videos
- समान्तर श्रेढ़ी BOOK - NOOTAN HINDICHAPTER - समान्तर श्रेढ़ी EXERCISE - प्रश्नावली 5.2
21 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )
14 Videos
- सांख्यिकीBOOK - NOOTAN HINDICHAPTER - सांख्यिकीEXERCISE - बहुविकल्पीय प्रश्न
7 Videos
Similar Questions
A.P.:121,117,113,.... कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
View Solutionk किस मान के लिए 2k−1,7 और 3k,A.P. में है?
View Solutionनिम्नलिखित सारणी में,रिक्त स्थानों को भरिए,जहाँ AP का प्रथम पद a सार्वान्तर d और n वां पद an है:
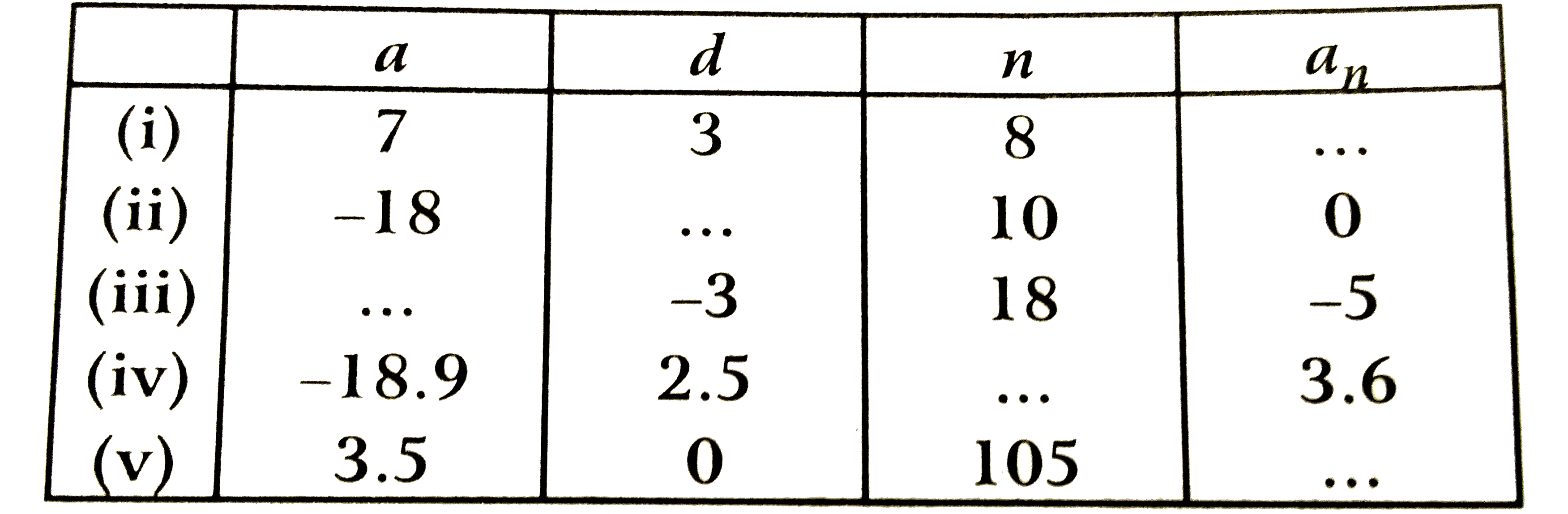
View Solutionयदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग R त्रिज्या के वृत्त की परिधि के बराबर है , तो :
View Solutionवर्गीकृत आंकड़ों का माध्य ज्ञात करने के लिए सूत्र ¯x=a+ΣfiΣfi में di निम्नलिखित के a विचलन है
View SolutionIf a1,a2,….an are in H.P then a1a2+,a3,…,an,a2a1+a3+….+an,…,ana1+a2+….+an−1
are in
View SolutionLet a1,a2,a3 …. an be in A.P. If 1a1an+1a2an−1+… + 1ana1=ka1+an(1a1+1a2+….1an) , then k is equal to :
View Solutionयदि a1,a2,a3..........,an समान्तर श्रेणी में हो, तो दर्शाइए की
1a1a2+1a2a3+1a3a4+.........+1an−1an=n−1a1an.
View Solutionयदि a1,a2,a3,........,an समांतर श्रेणी में हो, तो दर्शाइए की
1a1an+1a2an−1+.........+1ana1=2a1+an(1a1+1a2+.......+1an)
View Solutionan ಈ ಕೆಳಗಿನಂತೆ ನಿರೂಪಿಸಲ್ಪಟ್ಟಾಗ a1,a2,...,an,....ಕ ನಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ.ಎಂದು ತೋರಿಸಿ. an=3+4n
View Solutionan ಈ ಕೆಳಗಿನಂತೆ ನಿರೂಪಿಸಲ್ಪಟ್ಟಾಗ a1,a2,...,an,.... ಕ ನಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ.ಎಂದು ತೋರಿಸಿ. an=9−5n
View Solutiona_n క్రింది విధంగా నిర్వచించబడితే a1, a2, ....,an, అంకశ్రేఢి అవుతుందని చూపండి. మరియు మొదటి 15 పదాల మొత్తమును కనుగొనండి. an=3+4n
View Solutionan క్రింది విధంగా నిర్వచించబడితే a1, a2, ....,an, అంకశ్రేఢి అవుతుందని చూపండి. మరియు మొదటి 15 పదాల మొత్తమును కనుగొనండి. an=9−5n
View SolutionShow that a1,a2,...,an,...form an AP where an is defined as below :
(i) an=3+4n
(ii) an=9−5n.
Also find the sum of the first 15 terms in each case.
View SolutionIf a1,a2,......,an>0, then prove that a1a2+a2a3+a3a4+.....+an−1an+ana1>n
View SolutionIf a1,a2,,an are in H.P., then a1a2+a3++an,a2a1+a3++an,,ana1+a2++an−1 are in a. A.P b. G.P. c. H.P. d. none of these
View Solution
