O केन्द्र के वृत्त में, यदि एक बाह्य बिन्दु B से दो स्पर्श रेखाएँ BC और BD इस प्रकार खींची जाती है कि ∠DBC=120∘ है , तो सिद्ध कीजिए कि BC+BD=BO.
∠1+∠2=120∘ (दिया है)
परन्तु ∠1+∠2 (स्पर्श रेखायें केन्द्र पर समान कोण अन्तरित करती है)
∴∠1+∠1=120∘
⇒2∠1=120∘
⇒∠1=60∘
तथा, ∠OCB=90∘
(स्पर्श बिन्दु से जाने वाली त्रिज्या स्पर्श रेखा पर लम्ब होती है)
अब समकोण ΔOCB में,
cos60∘=BCOB

⇒12=BCOB
∴OB=2BC ⇒OB=BC+BC
⇒OB=BC+BD (∵ एक बाह्य बिन्दु से खींची स्पर्श रेखायें बराबर होती है।)
Topper's Solved these Questions
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली
29 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10.1
4 Videos
- वास्तविक संख्याएँBOOK - NOOTAN HINDICHAPTER - वास्तविक संख्याएँEXERCISE - विविध प्रश्नावली
30 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )
14 Videos
Similar Questions
एक वृत्त की त्रिज्या 8 सेमी है। इसके केन्द्र से 10 सेमी की दुरी पर स्थित बिन्दु से वृत्त पर खींची स्पर्श रेखा की लम्बाई ज्ञात कीजिए।
View Solutionएक वृत्त की कितनी स्पर्श रेखाएँ हो सकती है?
View Solutionयूक्लिड विभाजन प्रमेयिका बताइए।
View Solutionयदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग R त्रिज्या के वृत्त की परिधि के बराबर है , तो :
View SolutionIf from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO.
View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
View Solutionदिये गए चित्र में,बाह्य बिंदु A से वृत्त कि दो स्पर्श AB व AC खींची गई है। ∠BAC=48∘ हो ,तो ∠ABC का मान लिखिए।
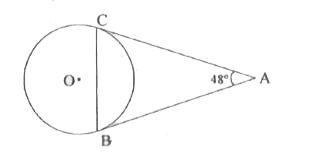
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionयदि बिन्दु (a,b),(a',b') और (a−a',b−b') संरेख हो तो सिद्ध कीजिए कि
ab'=a'b.
साथ ही यह भी सिद्ध कीजिए कि इन बिन्दुओं से होकर जाने वाली रेखा मुलबिन्दु से होकर जाती है।
View Solutionयदि A और B दो वर्ग आव्यूह इस प्रकार हैं कि AB = A और BA = B तो सिद्ध करो कि A और B समशम होंगे |
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solution
