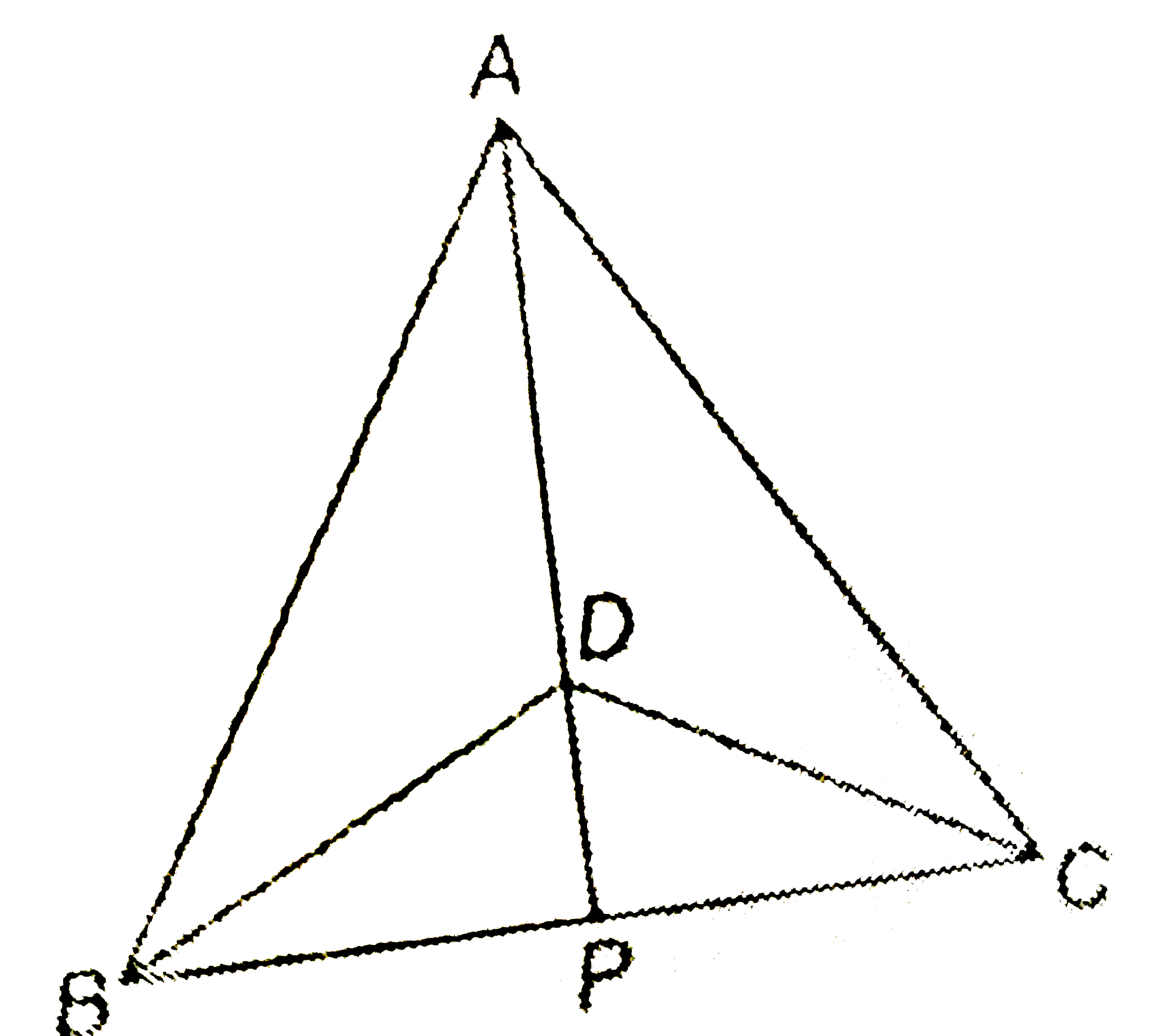
ΔABC और ΔDBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार है कि A और D भुजा BC के एक ही ओर स्थित है (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP, कोण A और कोण D दोनों को समद्विभाजित करता है।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक है।

ΔABC और ΔDBC दो समद्विबाहु त्रिभुज समान आधार BC पर इस प्रकार है कि AB=AC और DB=DC.
दर्शाना है :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
AP,∠A और ∠D दोनों से समद्विभाजित करता है।
(iv) AP, BC का लम्ब समद्विभाजक है।
उपपत्ति : (i) ΔABD और ΔACD में,
AB=AC (दिया है )
BD=CD (दिया है )
और AD=AD (उभयनिष्ठ)
∴ΔABD≅ΔACD (S.S.S.)
(ii) ΔABP और ΔACP में,
AB=AC (दिया है)
∠1=∠2 (∵ΔABD≅ACD)
और AP=AP (उभयनिष्ठ )
∴ΔABP≅ΔACP (S.S.S.)
(iii) ∠1=∠2 (∵ΔABD≅ΔACD)
⇒AP,∠A का समद्विभाजक है।
∠ADB=∠ADC (∵ΔABD≅ΔACD)
⇒180∘−∠ADB=180∘−∠ADC
⇒∠BDP=∠CDP (रैखिक युग्म अभिगृहीत से)
⇒AP,∠D का समद्विभाजक है।
(iv) BP=CP (∵ΔABP≅ΔACP)
और ∠3=∠4 ......(1)
परन्तु, ∠3+∠4−180∘ (रैखिक युग्म अभिगृहीत से )
∴∠3+∠3=180∘⇒∠3=90∘
[समीकरण (1) से ]
⇒∠3=∠4=90∘
अतः AP, BC का लम्ब समद्विभाजक है।
Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.4
6 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.5 ( ऐच्छिक)
4 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - प्रश्नावली 7.2
8 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- दो चरों वाले रैखिक समीकरण BOOK - NOOTAN HINDICHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - विविध प्रश्नावली
12 Videos
Similar Questions
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लम्बी भुजा होती है।
View SolutionABC एक त्रिभुज है। इसके अभ्यन्तर में एक ऐसा बिन्दु ज्ञात कीजिए जो ΔABC के तीनो शीर्षो से समदूरस्थ है।
View Solutionएक समद्विबाहु त्रिभुज ABC में, जिसमे AB = AC है, ∠A और ∠C के समद्विभाजक परस्पर बिन्दु O पर प्रतिच्छेद करते है। A और O को जोड़िए। दर्शाइए कि
(i) OB= OC
(ii) AO कोण A को समद्विभाजित करता है।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionx अक्ष का समीकरण लिखिय|
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि बिंदुओं A और B के स्थिति सदिश क्रमशः ¯a और ¯b हों तो उस बिंदु C का स्थिति सदिश ज्ञात कीजिए जो BA को आगे बढ़ने पर इस प्रकार स्थित है कि BC=1.5BA.
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
View SolutionABCD is a cyclic quadrilateral such that its sides AD and BC produced meet at P and sides AB and DC produced meet at Q. If angle A=62^@ and angle ABC= 74^@ , then the difference between angle P and angle Q is: ABCD एक चक्रीय चतुर्भुज है जो इस प्रकार है कि इसकी भुजाओं AD और BC को बढ़ाने पर वे P पर मिलती हैं तथा AB और DC को बढ़ाने पर वे Q पर मिलती हैं | यदि angle =62^@ और angle ABC= 74^@ है, तो angle P और angle Q के बीच अंतर ज्ञात करें |
View Solutiontriangle ABC is a triangle, where angle B is obtuse. AD is perpendicular on CB produced at D. If AB = 8cm, BC = 7cm and BD = 4cm, then AC is equal to : ABC एक त्रिभुज है, जिसमें कोण B अधिक कोण है | AD, CB पर लम्ब है जिसे D पर डाला गया है | यदि AB =8 सेमी, BC = 7 सेमी और BD = 4 सेमी है, तो AC किसके बराबर है ?
View Solution
