दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखण्ड परस्पर समद्विभाजित करते हैं।
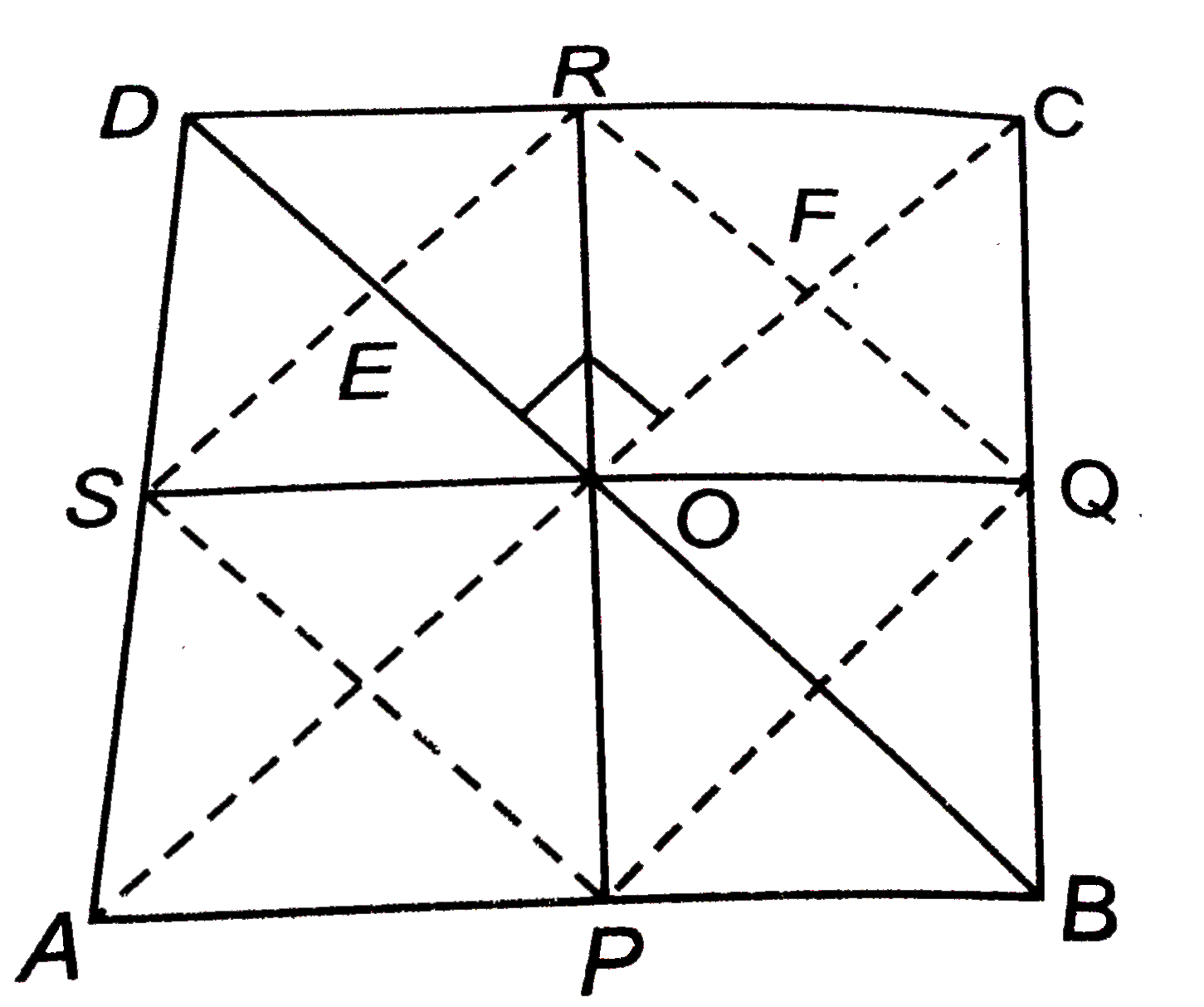
माना ABCD एक चतुर्भुज है और P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु है अर्थात AS=SD,AP=BP,BQ=CQ और CR=DR
हमें सिद्ध करना है कि PR और SQ एक-दूसरे को समद्विभाजित करते हैं अर्थात SO=OQ और PO=OR अब ΔADC में S और R क्रमशः AD और CD के मध्य –बिंदु है।
हम जानते हैं कि एक त्रिभुज में दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समांतर होता है।
∴SR∣∣AC और SR=12AC
(मध्य बिंदु प्रमेय से)………..1
इसी प्रकार ΔABC में P और Q क्रमशः AB और BC के मध्य-बिंदु है।
∴PQ∣∣AC और PQ=12AC
(मध्य बिंदु प्रमेय से)………….2
समीकरण 1 और 2 से
PQ∣∣SR और PQ=S=12AC
चतुर्भुज PQRS एक समांतर चतुर्भुज है जिसके विकर्ण SQ और PR हैं। हम यह भी जानते हैं कि समांतर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं। अतः SQ और PQ एक-दूसरे को समद्विभाजित करते हैं।
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली24videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8.112videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न5videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )8videos
त्रिभुज
Similar Questions
एक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
04:29View Solutionएक चतुर्भुज के कोण 3:5:9:13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
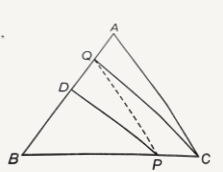
07:31View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
 02:47View Solution
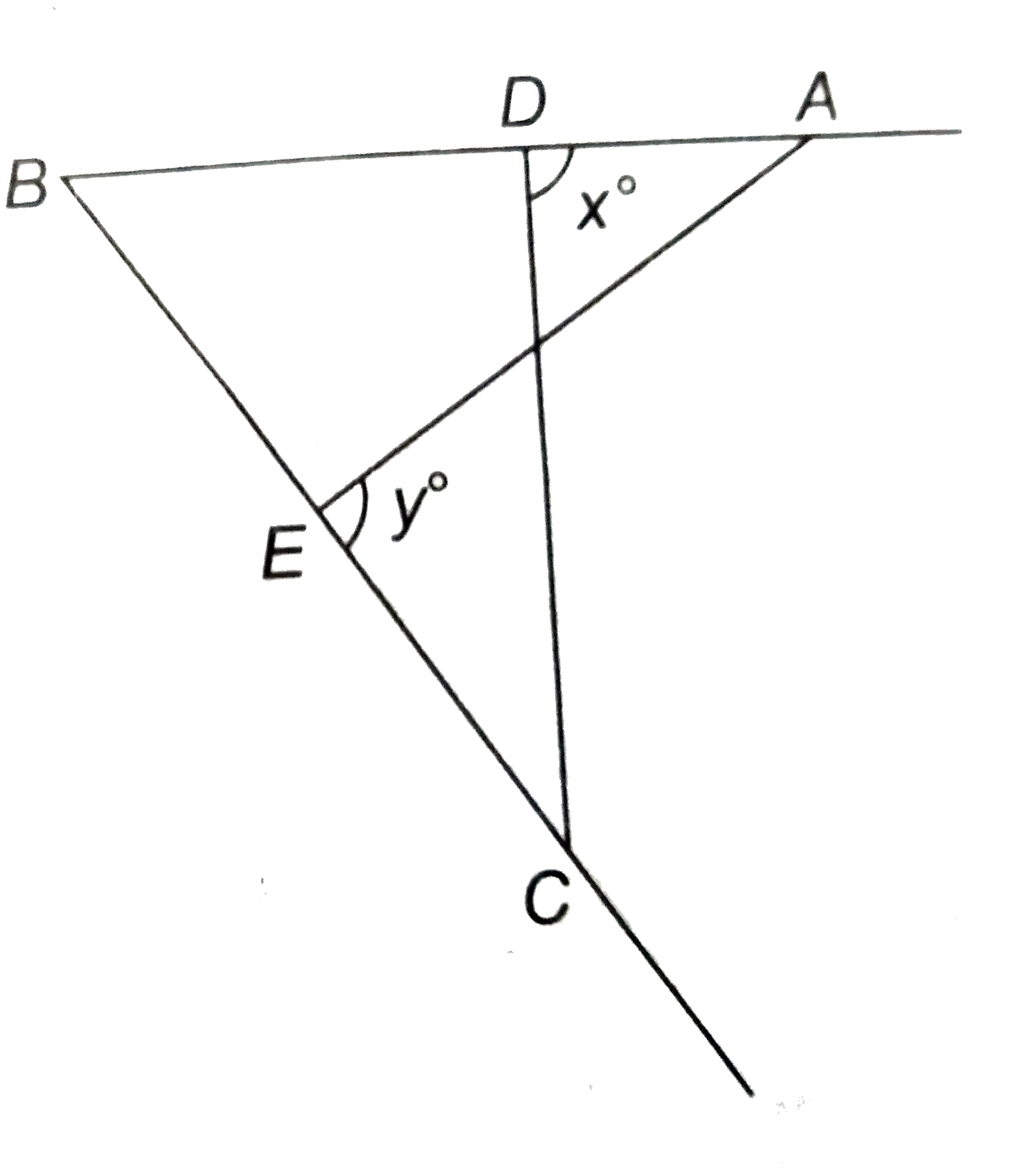
02:47View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
 04:27View Solution
04:27View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
04:39View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
06:12View Solution10सेमी त्रिज्या वाले वृत्त की त्रिज्याओं के मध्य बिन्दुओ का बिन्दुपथ होगा।
04:36View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
06:21View SolutionΔABC की भुजाओं के मध्यबिंदु D,E,F हैं। यदि O कोई बिंदु हो तो दर्शाइए कि
¯¯¯¯¯¯OE+¯¯¯¯¯¯OF+¯¯¯¯¯¯DO=¯¯¯¯¯¯OA02:27View Solutionदिखाइए कि किसी त्रिभुज में भुजाओं के लम्ब अर्धक संगामी होते हैं |
06:19View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
04:18View Solutionकिसी त्रिभुज ABC की माध्यिकाएँ AD, BE, CF बिन्दु G पर मिलती हैं | दर्शाइए कि :
ΔAGB=ΔBGC=ΔCGA=13ΔABC.04:56View Solutionसिद्ध कीजिए कि बिंदुओं (2,3) और(3,4) को मिलाने वाले रेखाखण्ड के मध्य बिंदु के निर्देशांक x और y निम्नलिखित समीकरण को संतुष्ट करते है :
x−y+1=0.03:33View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
03:53View Solutionबिन्दुओं (3,4) और (7,8) को मिलाने वाले रेखाखण्ड को रेखा 2x+3y+7=0 किस अनुपात में विभक्त करती है?
04:09View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
View Solution

