यदि किसी चतुर्भुज का प्रत्येक विकर्ण उस चतुर्भुज को बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है, तो सिद्ध कीजिए कि वह चतुर्भुज एक समान्तर चतुर्भुज होगा।
माना चतुर्भुज ABCD के विकर्ण AC और BD है।
प्रश्नानुसार विकर्ण AC,□ABCD को दो बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित करता है।
∴ΔABC का क्षेत्रफल =ΔACD का क्षेत्रफल
⇒ΔABC का क्षेत्रफल =12×□ABCD का क्षेत्रफल ...(1)
इसी प्रकार विकर्ण BD,□ABCD को दो बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित करता है।
∴ΔABD का क्षेत्रफल =ΔBCD का क्षेत्रफल
⇒ΔABD का क्षेत्रफल =12×□ABCD का क्षेत्रफल ...(2)
समीकरण (1) और (2) से
ΔABC का क्षेत्रफल =ΔABD का क्षेत्रफल
परन्तु ΔABC और ΔABD का एक ही आधार AB है।
∴ इनकी संगत ऊँचाइयाँ समान होगी।
implies AB और DC समान्तर है।
इसी प्रकार सिद्ध कर सकते है कि AD और BC समान्तर है।
∴□ABCD एक समान्तर चतुर्भुज है।

Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली
27 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.1
1 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
एक समान्तर चतुर्भुज का आधार, संगत शीर्षलम्ब का 3 गुना है। यदि समान्तर चतुर्भुज का क्षेत्रफल 48 वर्ग सेमी है, तो समान्तर चतुर्भुज का आधार और संगत शीर्षफ़ल ज्ञात कीजिए।
View Solutionनिम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
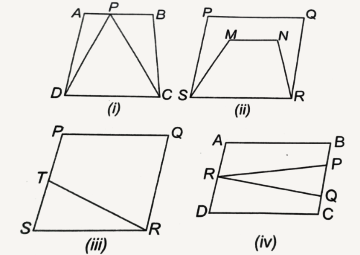
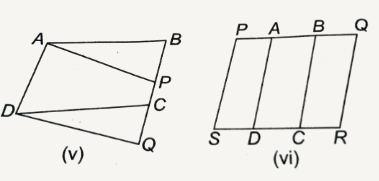
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionसमलम्ब चतुर्भुज एवं उसका क्षेत्रफल
View Solutionसामान्य चतुर्भुज का क्षेत्रफल |विशेष चतुर्भुजों का क्षेत्रफल
View SolutionRevision|चतुर्भुज#!#समान्तर चतुर्भुज पर आधारित प्रमेय#!#प्रमेय सिद्ध करना सीखे 45 Min
View SolutionRevision|चतुर्भुज#!#चतुर्भुज के प्रकार#!#समान्तर चतुर्भुज
View Solutionचतुर्भुज |चतुर्भुज का कोण योग गुण |प्रश्न |चतुर्भुज के प्रकार |महत्वपूर्ण बिन्दु |सारांश
View Solutionचतुर्भुज |चतुर्भुज का कोण योग गुण |चतुर्भुज के प्रकार |समांतर चतुर्भुज के गुण|प्रमेय|सारांश
View Solutionचतुर्भुज का कोण योग गुण |समांतर चतुर्भुज|प्रमेय|प्रश्न |सारांश
View Solutionसमांतर चतुर्भुज कअ क्षेत्रफल
View Solutionचतुर्भुज#!#चतुर्भुज के कोण योग का गुण
View Solution
