ΔABC की भुजा BC पर एक बिन्दु D इस प्रकार लिया गया है कि BD = 2DC है। सिद्ध कीजिए कि ar(ΔABD)=2ar(ΔADC).
ΔABC में, BD = 2DC
माना E, BD का मध्य-बिन्दु है।
तब, BE = ED = DC
∵ AE, ΔABD की माध्यिका है।
∴ar(ΔABE)=ar(ΔAED) …(1)
(त्रिभुज की माध्यिका इसे दो समान क्षेत्रफलों में विभाजित करती है)
पुनः AD,ΔAEC की माध्यिका है।
∴ar(ΔAED)=ar(ΔADC) ...(2)
(त्रिभुज की माध्यिका इसे दो समान क्षेत्रफलों में विभाजित करती है)
समीकरण (1) और (2) से
ar(ΔABE)=ar(ΔAED)=ar(ΔADC)=x (माना) ...(3)
अब ar(ΔABD)=ar(ΔABE)+ar(ΔAED)=x+x=2x=2×ar(ΔADC)

Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली
27 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.1
1 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
एक समान्तर चतुर्भुज का आधार, संगत शीर्षलम्ब का 3 गुना है। यदि समान्तर चतुर्भुज का क्षेत्रफल 48 वर्ग सेमी है, तो समान्तर चतुर्भुज का आधार और संगत शीर्षफ़ल ज्ञात कीजिए।
View Solutionनिम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
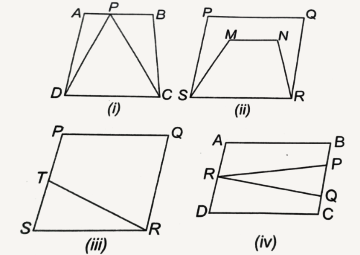
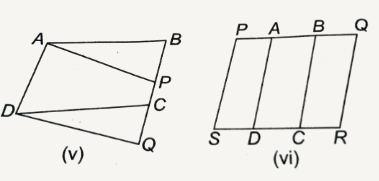
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View Solutionयदि त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार दिया गया है कि BD = 2DC , तो सिद्ध कीजिए कि ar(ΔABD)=2ar(ΔADC)
View SolutionIn ΔABC,B−D−C and BD=7,BC=20, then find followig ratios:
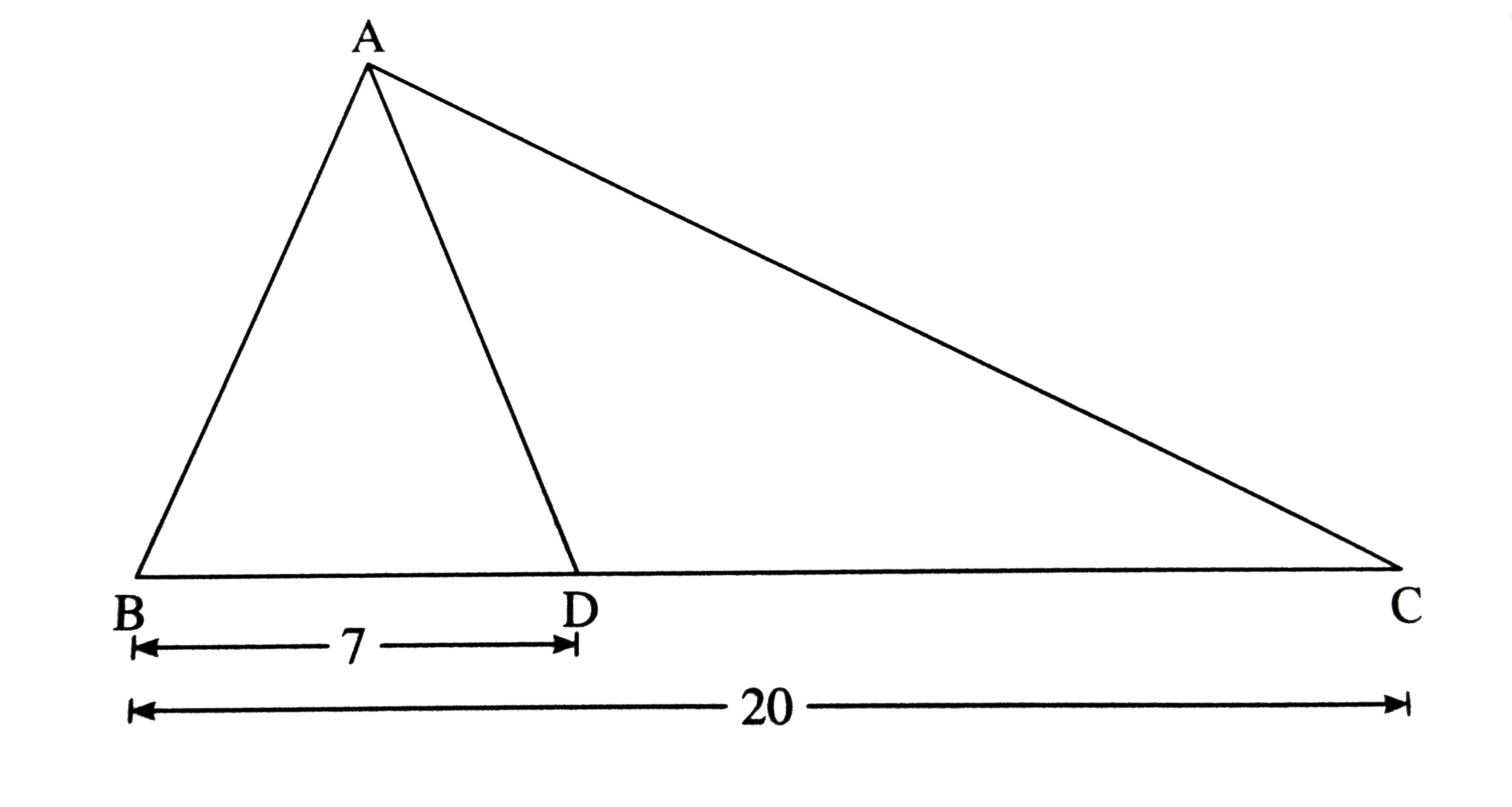
A(ΔABD)A(ΔADC)
A(ΔABD)A(ΔABC)
A(ΔADC)A(ΔABC)
View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
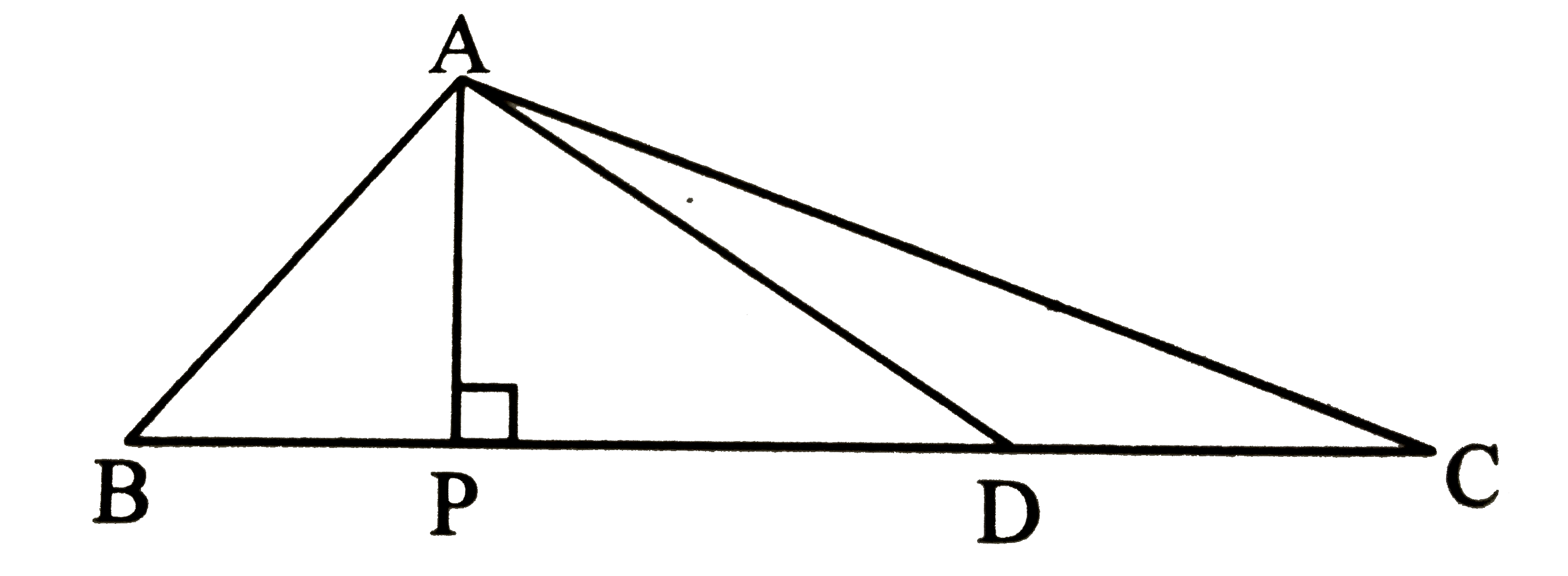
View SolutionIn ΔABC,point D is on side BC such that DC = 6, BC = 15. find
(i)A(ΔABD):A(ΔABC) and
(ii) A(ΔABD):A(ΔADC).
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solution
