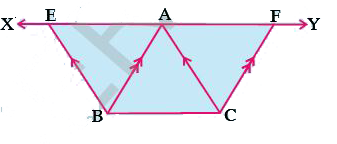
ΔABC में, BC के समान्तर रेखा XY है। यदि BE || AC और CF || AF, XY को क्रमशः E और F पर मिलते है, तो सिद्ध कीजिए कि ar(ΔABE)=ar(ΔACF)
∵BE||AC⇒BE||YC …(1)
और BC || EY (दिया है) …(2)
∴□BCYE एक समान्तर चतुर्भुज है। (∵ सम्मुख भुजाओं के युग्म समान्तर है)
अब ΔABE और समान्तर चतुर्भुज BCYE समान आधार EB और समान समान्तर रेखाओं EB और AC के मध्य स्थित है।
∴ar(ΔABE)=12ar(||gm BCYE) ...(3)
अब, CF || AB implies CF || BX
और BC || XF (दिया है)
∴□BCFX एक समान्तर चतुर्भुज है। (∵ सम्मुख भुजाओं के युग्म समान्तर है)
अब ΔACF और समान्तर चतुर्भुज BCFX समान आधार CF और समान समान्तर रेखाओं CF और AB के मध्य स्थित है।
∴ar(ΔACF)=12ar(||gm BCFX) ...(4)
परन्तु ar(||gm BCYE)=ar(||gm BCFX) ...(5)
(∵ समान्तर चतुर्भुज समान आधार BC और समान समान्तर रेखाओं BC और EF के मध्य स्थित है)
∴ समीकरण (3), (4) और (5) से
ar(ΔABE)=ar(ΔACF)

Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली
27 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.1
1 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
एक समान्तर चतुर्भुज का आधार, संगत शीर्षलम्ब का 3 गुना है। यदि समान्तर चतुर्भुज का क्षेत्रफल 48 वर्ग सेमी है, तो समान्तर चतुर्भुज का आधार और संगत शीर्षफ़ल ज्ञात कीजिए।
View Solutionनिम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
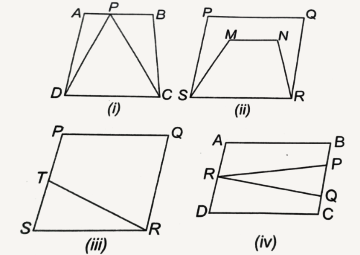
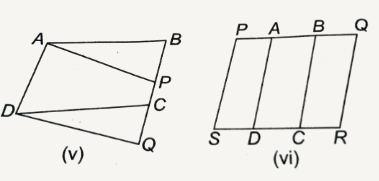
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionत्रिभुज ABC की भुजा BC के समांतर एक रेखा XY है। यदि BE ।। AC तथा CF ।। AB रेखा XY को क्रमशः E तथा F पर मिलते है तो सिद्ध कीजिए कि ar(ΔABE)=ar(ΔACF).
View SolutionΔABC कि भुजा BC के समांतर XY रेखा है, BE∣∣AC और CF∣∣AB खींचे जो XY को क्रमश : E और F पर काटती है । सिद्ध करे कि ar(ΔABE)=ar(ΔACF).
View Solutionसरल रेखा ax+by=c, xy- तल को कितने भागो में विभाजित करती है और वे कौन कौन से है ?
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionयदि बिंदुओं A और B के स्थिति सदिश क्रमशः ¯a और ¯b हों तो उस बिंदु C का स्थिति सदिश ज्ञात कीजिए जो BA को आगे बढ़ने पर इस प्रकार स्थित है कि BC=1.5BA.
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View SolutionIn the figure, XY is a line parallel to BC is drawn through A. If BE || CA and CF || BA are drawn to meet XY at E and F respectively. Show that ar(ΔABE)=ar(ΔACF).
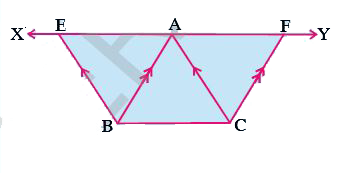
View SolutionIn the figure, XY is a line parallel to BC is drawn through A. If BE || CA and CF || BA are drawn to meet XY at E and F respectively. Show that ar(ΔABE)=ar(ΔACF).
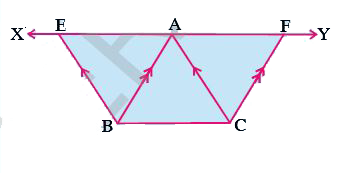
View SolutionIn the figure, XY is a line parallel to BC is drawn through A. If BE || CA and CF || BA are drawn to meet XY at E and F respectively. Show that ar(ΔABE)=ar(ΔACF).
View SolutionXY is a line parallel to side BC of a triangle ABC. If BE||AC and CF ||AB meet XY at E and F respectively , show that ar(ABE)=ar(ACF)

View SolutionIn triangle ABC , F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD bot BC and AD intersect FE at G, then GD: AG = ? triangle ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD bot BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View Solution
