निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए :
(a) |a+b|≤|a|+|b|
(b) |a+b|≥||a|−|b∣∣
(c) |A−b|≤|a|+|b|
(d) |A−b|≥||a|−|b∣∣
इनमें समीका ( समता ) का चिह्न कब लागू होता है ?
माना दो सदिशों a तथा b को त्रिभुज OPQ की क्रमशः भुजाओं OP तथा OQ द्वारा प्रदर्शित किया गया है तथा उसका परिमाण OQ सदिश (a+b) द्वारा प्रदर्शित किया गया है ।
( a ) त्रिभुज के गुणों से , किसी त्रिभुज की एक भुजा, उसकी शेष दो भुजाओं के योग से सदैव कम होती है ।
∴ΔOPQ में,
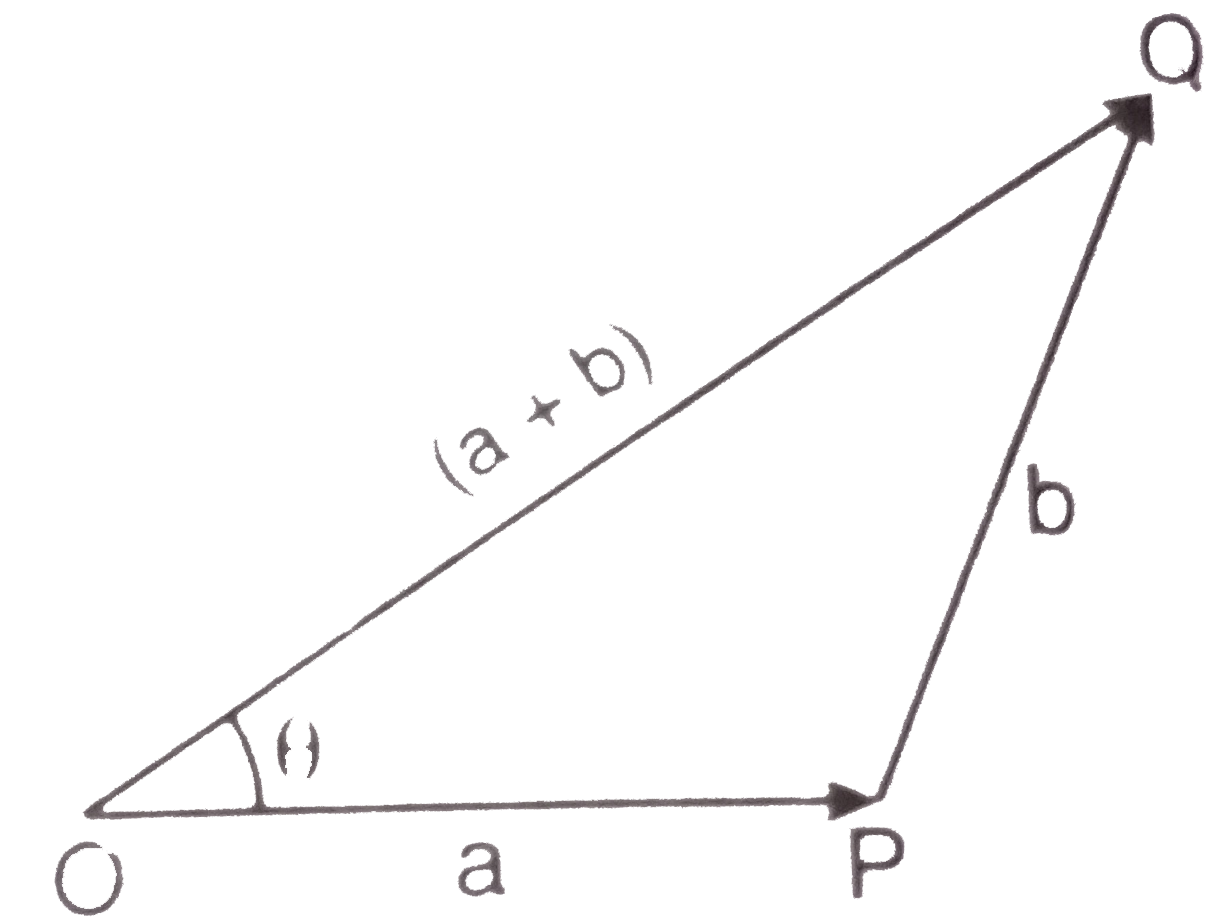
OQ<OP+PQ
|a+b|<|a|+|b| ...(i)
हम जानते हैं कि दो सदिशों के बीच कोण से प्राप्त परिणामी सदिश का परिमाण
|a+b|=√a2+b2+2abcosθ
यदि दोनों सदिश समान दिशा में कार्यरत हैं, तो θ=0
∴ |a+b|=√a2+b2+2ab (∴cosθ=1 जब θ=0)
=√(a+b)2
या |a+b|=|a|+|b| ...(ii)
समीकरण (i ) व (ii ) से,
|a+b|≤|a|+|b|
दोनों पक्ष समान होंगे जब दोनों सदिश a तथा b समान दिशा में एक ही रेखा के अनुदिश हों।
त्रिभुज के गुणों से त्रिभुज की एक भुजा शेष दो भुजाओं के अंतर से अधिक होती है।
अतः ΔOPQ में, OQ>|OP−PQ|
[नोट : यदि PQ OP से बड़ा है अर्थात PQ>OP तो यह ऋणात्मक हो सकता है।]
|a+b|>|a|−|b| ...(iii)
यदि दिए गए दोनों सदिश एक ही रेखा में विपरीत दिशा में कार्यरत हों, तब
|a+b|=|a|−|b| ...(iv)
समीरकण (i ) व (iv ) से,
यदि सदिश a व b एक ही सरल रेखा में परस्पर विपरीत दिशा में कार्यरत है तो समानता चिन्ह मान्य होगा ।
(c) यदि PR सदिश −b को तथा सदिश a व −b का परिणामी OR के द्वारा प्रदर्शित हो तब
त्रिभुज के गुणों से, किसी त्रिभुज की एक भुजा उसकी शेष दो भुजाओं की लम्बाइयों के योग से कम होती है।
∴ΔOPR में, OR<OP<PR
|a−b|<|a|+|−b|
परन्तु |−b|=|b|, क्योंकि किसी सदिश का परिमाण सदैव धनात्मक होता है।
या |a−b|<|a|+|b| ...(v)
यदि सदिश a तथा b एक सरल रेखा में परस्पर विपरीत दिशा में कार्यरत हैं, तो
|a−b|=|a|+|b| ...(vi)
समीकरण (v ) व (vi ) से,
|a−b|≤|a|+|b|
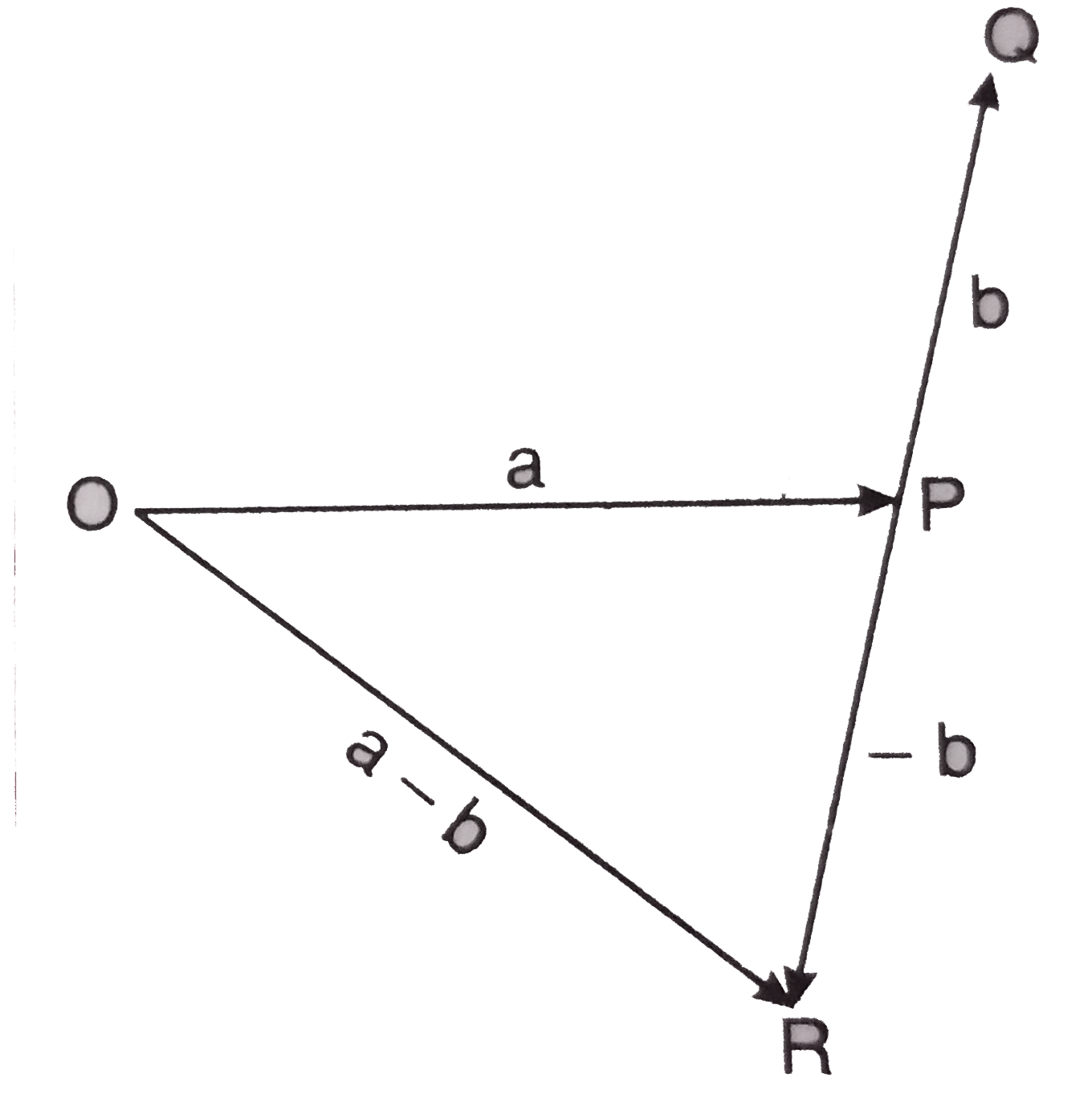
(d) त्रिभुज के गुणों से, त्रिभुज की भुजा इसकी शेष दो भुजाओं के अंतर से अधिक होती है।
∴ΔPQR में, OR>|OP−PR|
[पुनः (OP−PR) का परिमाण लिया गया है, क्योंकि PR, OP से अधिक हो सकता है।]
∴ |a−b|>|a|−|−b|
|a−b|>|a|−|b| ...(vii)
यदि सदिश a तथा b एक ही सरल रेखा में समान दिशा में हैं।
तब |a−b|>|a|−|b| ...(viii)
समीरकण (vii) व (viii) से,
|a−b|≥|a|−|b|
समानता चिन्ह मान्य होगा । यदि सदिश a व b एक ही सरल रेखा में समान दिशा में हों।
Topper's Solved these Questions
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - बोधात्मक प्रश्न
5 Videos
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - आंकिक प्रश्न
3 Videos
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - संख्यात्मक प्रश्न
37 Videos
- वृत्तीय गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - वृत्तीय गति EXERCISE - वस्तुनिष्ठ प्रश्न
33 Videos
- सरल रेखा में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - वस्तुनिष्ठ प्रश्न
52 Videos
Similar Questions
प्रक्षेप्य पथ के किस बिंदु पर चाल (i ) अधिकतम (ii ) न्यूनतम होती है?
View Solutionकिसी पिंड को किस प्रेक्षपण कोण पर फेंका जाए कि उसकी क्षैतिज परास ऊर्ध्वाधर ऊँचाई बराबर हों?
View Solutionएक कण पर 5 न्यूटन, 4 न्यूटन तथा 3 न्यूटन परिमाण के बल क्रमश : पूर्व,उत्तर तथा पश्चिम दिशाओं में लग रहे हैं । एक सदिश आरेख बनाकर परिणामी बल का परिणाम ज्ञात कीजिए तथा आरेख में इसकी दिशा अंकित कीजिए ।
View Solutionएकसमान क्षैतिज वृत्तीय गति में नियत रहता है :
View Solutionगैस के अणुओं की गति होती है :
View Solutionनिम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए:
(a) |a+b|≤|a|+|b|
(b) |a+b|≥||a|−|b∣∣
(c ) |a−b|≤|a|+|b|
(d) |a−b|≥||a|−|b∣∣
इनमे समीका (समता ) का चिन्ह कब लागु होता है ?
View Solutionसदिश a और b के बारे में निम्नलिखित असमिकाओ पर विचार कीजिएः
I.|a+b|≤|a|+|b| II. I.|a−b|≥|a|−|b|
उपरोक्त में कौन-सा सही है/है?
View Solutionयदि sin(A+B)=1 तथा cos(A−B)=1,0∘<A+B≤90∘ और A≥B हो , तो A तथा B के मान ज्ञात करो ।
View SolutionIf A, B are two events such that P(A∪B)≥34and18≤P(A∩B)≤38
View SolutionEstablish the following vector inequalities geometrically or otherwise :
(a) |a+b|≤|a|+|b|
(b) |a+b|≥||a|−|b∣∣
(c ) |a−b|≤|a|+|b|
(d) |a−b|≥||a|−|b∣∣
When does the equality sign above apply ?
View SolutionEstablish the following vector inequalities geometrically or otherwise : (a) |a+b|le|a|+|b| (b) |a+b|ge||a|-|b|| (c ) |a-b|le|a|+|b| (d) |a-b|ge||a|-|b|| When does the equality sign above apply ?
View SolutionEstablish the following vector inequalities geometrically or otherwise : (a) |a+b|le|a|+|b| (b) |a+b|ge||a|-|b|| (c ) |a-b|le|a|+|b| (d) |a-b|ge||a|-|b|| When does the equality sign above apply ?
View SolutionEstablish the following vector inequalities geometrically or otherwise :
(a) |a+b|≤|a|+|b|
(b) |a+b|≥||a|−|b∣∣
(c ) |a−b|≤|a|+|b|
(d) |a−b|≥||a|−|b∣∣
When does the equality sign above apply ?
View Solutionयदि A, B दो घटनायें इस प्रकार है कि P(A∪B)≥34 तथा 18≤P(A∩B)≤38 तो
View SolutionIf A and B are arbitrary events, then a) P(A∩B)≥P(A)+P(B) (b) P(A∪B)≤P(A)+P(B) (c) P(A∩B)=P(A)+P(B) (d)None of these
View Solution
