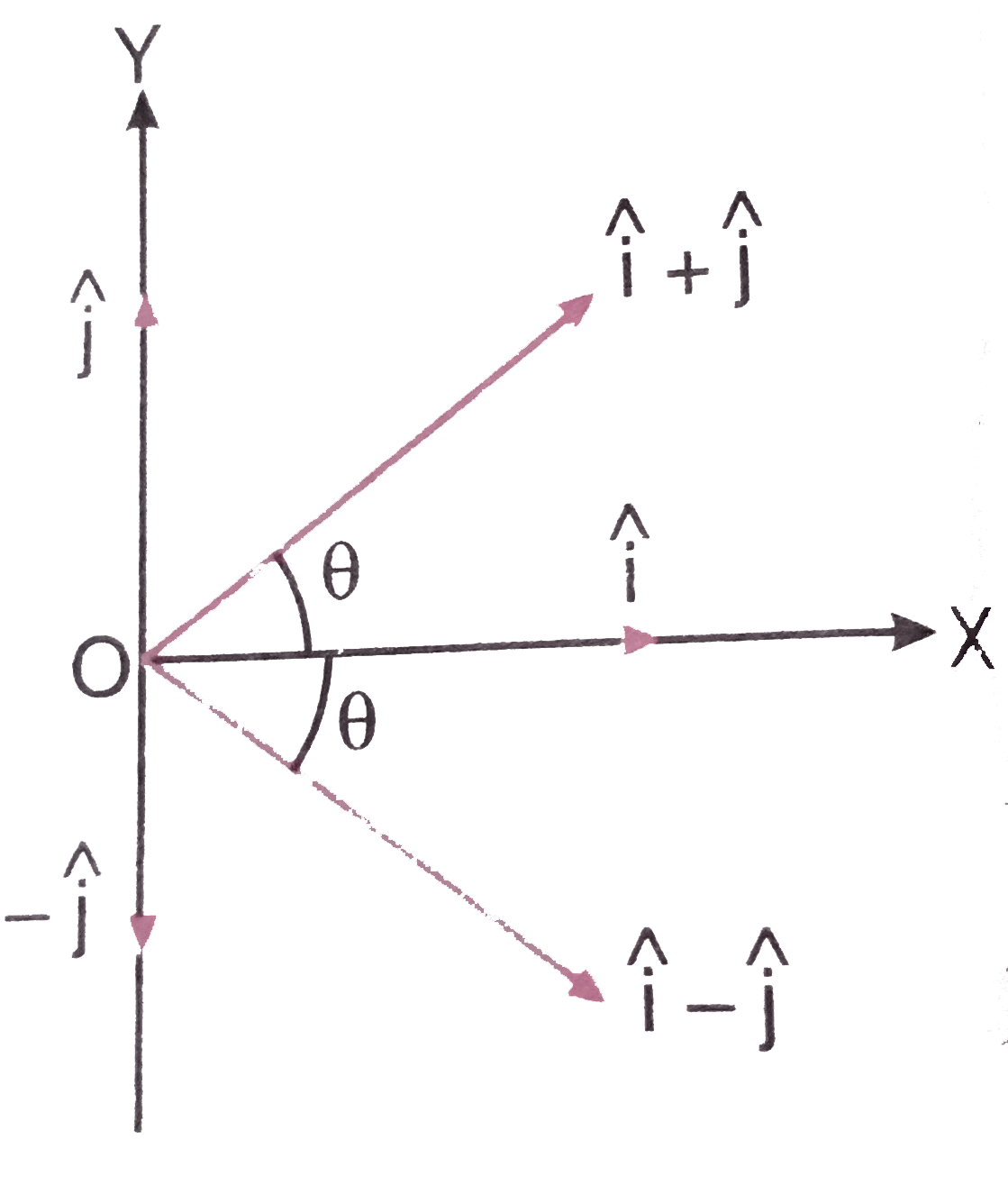
ˆi व ˆj क्रमशः x व y - अक्षों के अनुदिश एकांक सदिश हैं। सदिशों ˆi+ˆj तथा ˆi−ˆj का परिमाण तथा दिशा क्या होगी? सदिश A=2ˆi+3ˆj के ˆi+ˆj व ˆi−ˆj के दिशाओं के अनुदिश घटक निकालिए। [ आप ग्राफी विधि का उपयोग कर सकते हैं ]
(i) (ˆi+ˆj) का परिमाण
∣∣ˆi+ˆj∣∣=√(1)2+(1)2=√2
यदि (ˆi+ˆj), x - अक्ष के साथ θ कोण बनाता है
तो (ˆi+ˆj).ˆi=∣∣(ˆi+ˆj)∣∣.∣∣ˆi∣∣cosθ
या ˆi.ˆi+ˆj.ˆi=√2.1.cosθ
1+0=√2.cosθ
(चूँकि ˆi.ˆi=1,ˆj.ˆi=0)
cos.θ=1√2=cos45∘
या θ=45∘
अतः (ˆi+ˆj), x - अक्ष के साथ 45∘ का कोण बनाता है।
अब (ˆi−ˆj) का परिमाण
∣∣ˆi+ˆj∣∣=√(1)2+(−1)2=√2.
अब यदि (ˆi−ˆj), x -अक्ष के साथ θ कोण बनाता है, तो
(ˆi−ˆj).ˆi=∣∣(ˆi−ˆj)∣∣.∣∣ˆi∣∣cosθ
ˆi.ˆi−ˆj.ˆi=√2cosθ
या 1−0=√2cosθ
csoθ=1√2=cos45∘
या θ=−45∘ [चूँकि (ˆi−ˆj) चतुर्थांश में होगा]
(ii) (ˆi+ˆj) की दिशा में एकांक सदिश =(ˆi+ˆj)∣∣ˆi+ˆj∣∣=(ˆi+ˆj)√2
अतः सदिश →A का (ˆi+ˆj) दिशा में घटक का परिमाण
→A.(ˆi+ˆj)=(2ˆi+3ˆj).(ˆi+ˆj)
=2ˆi.ˆi+2ˆi.ˆj+3ˆj.ˆi+3ˆj.ˆj
=2+0+0+3=5
∴→A का (ˆi+ˆj) की दिशा में घटक
ˆi+ˆj√2.5=5√2(ˆi+ˆj), (चूँकि ˆa=→a|→a|)
अब (ˆi−ˆj) की दिशा में एकांक सदिश =(ˆi−ˆi)∣∣ˆi−ˆj∣∣=ˆi−ˆj√2
अब सदिश →A का (ˆi−ˆj) की दिशा में घटक का परिमाण
→A.(ˆi−ˆj)=(2ˆi+3ˆj)(ˆi−ˆj)
=2ˆi.ˆi−2ˆi.ˆj+3ˆj.ˆi−3ˆj.ˆj
=2−0+0−3=−1
अतः →A का (ˆi−ˆj) की दिशा में घटक =ˆi−ˆj√2×(−1)
=(−ˆi+ˆj)√2
Topper's Solved these Questions
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - बोधात्मक प्रश्न
5 Videos
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - आंकिक प्रश्न
3 Videos
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - संख्यात्मक प्रश्न
37 Videos
- वृत्तीय गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - वृत्तीय गति EXERCISE - वस्तुनिष्ठ प्रश्न
33 Videos
- सरल रेखा में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - वस्तुनिष्ठ प्रश्न
52 Videos
Similar Questions
प्रक्षेप्य पथ के किस बिंदु पर चाल (i ) अधिकतम (ii ) न्यूनतम होती है?
View Solutionकिसी पिंड को किस प्रेक्षपण कोण पर फेंका जाए कि उसकी क्षैतिज परास ऊर्ध्वाधर ऊँचाई बराबर हों?
View Solutionएक कण पर 5 न्यूटन, 4 न्यूटन तथा 3 न्यूटन परिमाण के बल क्रमश : पूर्व,उत्तर तथा पश्चिम दिशाओं में लग रहे हैं । एक सदिश आरेख बनाकर परिणामी बल का परिणाम ज्ञात कीजिए तथा आरेख में इसकी दिशा अंकित कीजिए ।
View Solutionएकसमान क्षैतिज वृत्तीय गति में नियत रहता है :
View Solutionगैस के अणुओं की गति होती है :
View Solution(hati+hatj)xx(hati-hatj)=
View Solutionयदि सदिश 2ˆi+ˆj+ˆk तथाˆi−ˆj+λ लम्बवत है , तब λ=
View Solutionसिद्ध कीजिएः कि [ˆi,ˆj,ˆk]=1व[ˆi,ˆj,ˆk]=−1
View Solution[ˆiˆkˆj]+[ˆkˆjˆi]+[ˆjˆkˆi] is equal to
View Solution[ˆiˆkˆj]+[ˆkˆjˆi]+[ˆjˆkˆi] is equal to
View Solutionसदिशों →a=2ˆi+4ˆj−5ˆk और →b=λˆi+2ˆj+3ˆk के योग के अनुदिश एकांक सदिश के साथ सदिश ˆi+ˆj+ˆk का अदिश गुणनफल 1 के बराबर होता है। λ का मान ज्ञात कीजिए।
View Solutionयदि A, B, C, D बिंदुओं के स्थित सदिश क्रमशः ˆi+ˆj−ˆk,2ˆi−ˆj+3ˆk,2ˆi−3ˆk,3ˆi−2ˆj+ˆk है तो ¯¯¯¯¯¯AB का ¯¯¯¯¯¯CD अनुदिश प्रक्षेप ज्ञात कीजिए |
View Solutionपरिमाण 10√3 के सभी सदिश ज्ञात कीजिए जो सदिशों ˆi+2ˆj+ˆk और −ˆi+3ˆj+4ˆk के समतल पर लम्ब हैं |
View Solutionसंतालों →r⋅(2ˆi+3ˆj+4ˆk) तथा →r⋅(ˆi+ˆj)=4 के बिच का कोण ज्ञात कीजिए |
View Solutionसदिश 2ˆi−ˆj तथा ˆi+2ˆj के मध्य का कोण ज्ञात कीजिये।
View Solutionसदिश 4ˆi−ˆj+3ˆk तथा −2ˆi+ˆj−2ˆk के लम्बवत 9 इकाई परिमाण वाला सदिश ज्ञात किजिए।
View Solution