कोई लड़ाकू जहाज 1.5 किमी की ऊँचाई पर 720 किमी/घंटा की चाल से क्षैतिज दिशा में उड़ रहा है और किसी वायुयान भेदी तोप के ठीक ऊपर से गुजरता है । ऊर्ध्वाधर से तोप की नाल का क्या कोण हो जिससे 600 मीटर/सेकंड−1 की चाल से दागा गया गोला वायुयान पर वार कर सके । वायुयान के चालक को किस न्यूनतम ऊँचाई पर जहाज को उड़ाना चाहिए । जिससे गोला लगने से बच सके । (g = 10 मीटर/सेकंड2)
प्रश्नानुसार , लड़ाकू जहाज का वेग y = 720 किमी/घंटा =720×518 मीटर/सेकंड = 200 मीटर/सेकंड
लड़ाकू जहाज की ऊँचाई = 1.5 किमी = 1500 मीटर , तथा गोले की चाल →u=600 मीटर/सेकंड
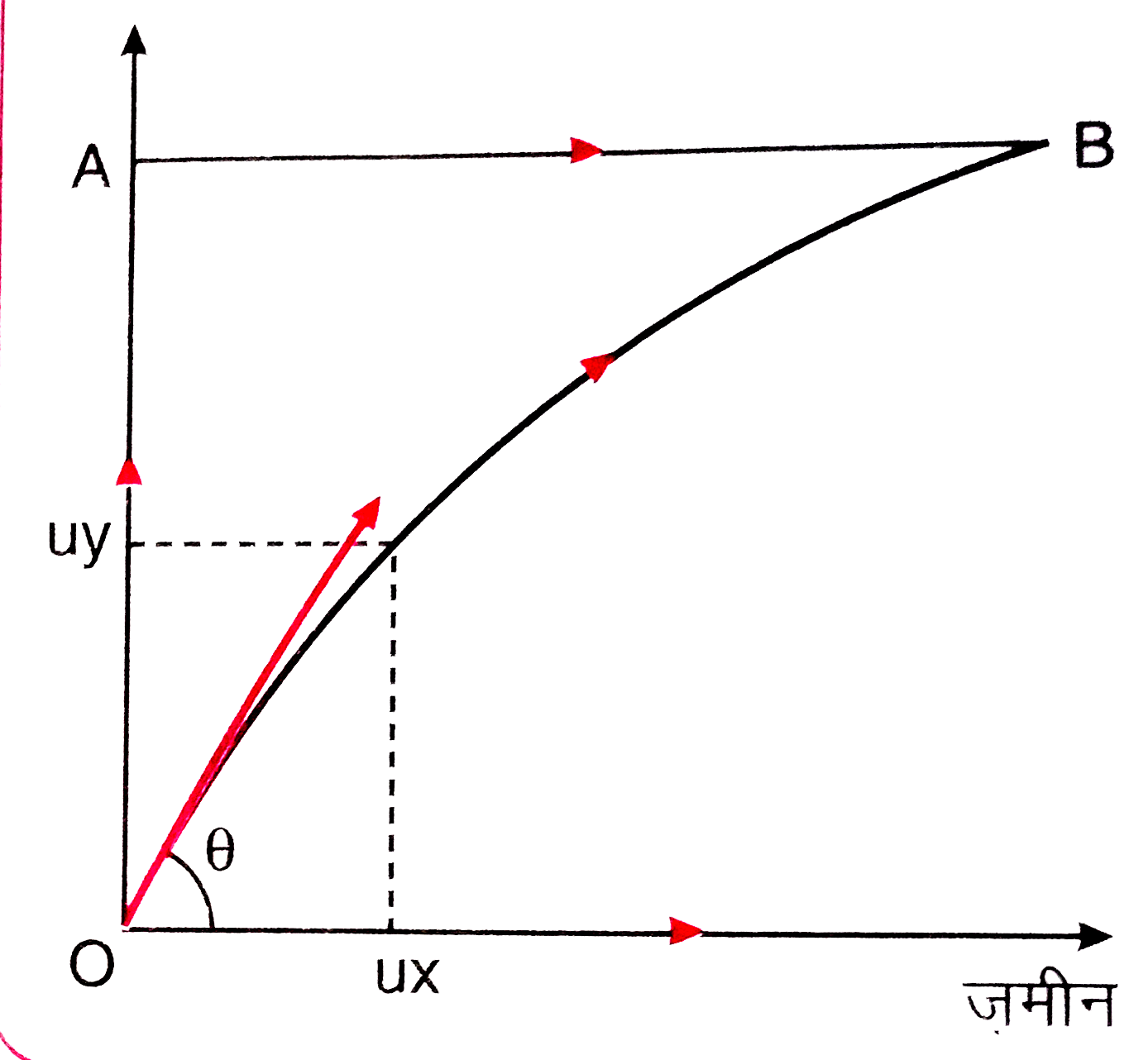
यदि जमीन पर वायुयान भेदी तोप की स्थिति O तथा क्षैतिज दिशा में उड़ रहे लड़ाकू जहाज की स्थिति A है ( चित्र 4.58 ) ।
अब यदि तोप से गोला ऊर्ध्वाधर से θ कोण पर दागा जाता है, तो →u का क्षैतिज घटक ux=ucosθ
यदि गोला , लड़ाकू जहाज से बिंदु B पर t समय बाद टकराता हैं तो चाल v से समय t में क्षैतिज दिशा में गति कर रहे लड़ाकू जहाज की क्षैतिज दूरी , चाल vx से समान समय t में गोले द्वारा तय की गयी क्षैतिज दूरी बराबर होगी |
अर्थात v×t=ucosθ×t
या cosθ=vu
=200600=13=0.333
या θ=70.5∘
ऊर्ध्वाधर से कोण =90−70.5=19.5∘.
लड़ाकू जहाज को वायुयान भेदी तोप से बचने के लिए, गोले द्वारा प्राप्त अधिकतम ऊँचाई h से अधिक ऊँचाई पर उड़ना चाहिए ।
h=u2sin2θ2g=(600)2sin2(70.5)2×10
=(600)2×(0.943)22×10
=16006.4 मीटर (या लगभग 16 किमी)
अतः लड़ाकू जहाज को वायुयान भेदी तोप से दागे गए गोले से बचने के लिए न्यूनतम 16 किमी ऊँचाई पर उड़ाना चाहिए ।
Topper's Solved these Questions
- समतल में गति Book:SHIVLAAL PUBLICATIONChapter:समतल में गति Exercise:बोधात्मक प्रश्न
Explore 5 Videos
- समतल में गति Book:SHIVLAAL PUBLICATIONChapter:समतल में गति Exercise:आंकिक प्रश्न
Explore 3 Videos
- समतल में गति Book:SHIVLAAL PUBLICATIONChapter:समतल में गति Exercise:संख्यात्मक प्रश्न
Explore 37 Videos
- वृत्तीय गति Book:SHIVLAAL PUBLICATIONChapter:वृत्तीय गति Exercise:वस्तुनिष्ठ प्रश्न
Explore 33 Videos
- सरल रेखा में गति Book:SHIVLAAL PUBLICATIONChapter:सरल रेखा में गति Exercise:वस्तुनिष्ठ प्रश्न
Explore 52 Videos
Similar Questions
प्रक्षेप्य पथ के किस बिंदु पर चाल (i ) अधिकतम (ii ) न्यूनतम होती है?
View Solutionकिसी पिंड को किस प्रेक्षपण कोण पर फेंका जाए कि उसकी क्षैतिज परास ऊर्ध्वाधर ऊँचाई बराबर हों?
View Solutionएक कण पर 5 न्यूटन, 4 न्यूटन तथा 3 न्यूटन परिमाण के बल क्रमश : पूर्व,उत्तर तथा पश्चिम दिशाओं में लग रहे हैं । एक सदिश आरेख बनाकर परिणामी बल का परिणाम ज्ञात कीजिए तथा आरेख में इसकी दिशा अंकित कीजिए ।
View Solutionएकसमान क्षैतिज वृत्तीय गति में नियत रहता है :
View Solutionगैस के अणुओं की गति होती है :
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक वायु सेना का जहाज 100 किमी/घण्टा की दर से ऊर्ध्वाधरतः ऊपर की और चढ़ रहा है। यदि पृथ्वी की त्रिज्या r किमी है , तब इसके उड़ना शुरू के मिनट बाद जहाज से दिखाई देने वाले पृथ्वी का क्षेत्रफल A=2πr2hr+h जहाँ , h जहाज की पृथ्वी से दूरी है )
View SolutionIf a boat goes upstream at a speed fo 18 km /hr and comes back the same distance at 30 km/ hr.What is the average speed (in km /hr)for the total journey?
कोई नाव धारा के विपरीत दिशा में 10 किलोमीटर /घंटा की चाल से चलती है और समान दूरी पर 30 किलोमीटर/घंटा की चाल से वापस आती है। कुल यात्रा के लिए औसत चाल किलोमीटर/ घंटा में) क्या है?
View SolutionAn aeroplane flying horizontally at a height of 3 Km. above the ground is observed at a certain point on earth to subtend an angle of 60^@ . After 15 sec flight, its angle of elevation is changed to 30^@ . The speed of the aeroplane (taking sqrt3 = 1.732) is- कोई वायुयान पृथ्वी की सतह से 3 कि.मी. ऊपर क्षेतिज उड़ रहा है। पृथ्वी से किसी बिन्दु से यह देखने में आता है कि वह 60^@ के कोण पर कक्षांतरित होता है। 15 सेकण्ड बाद उसका उन्नयन कोण 30^@ परिवर्तित हो जाता हैं वायुयान की चाल बताइए। ( sqrt3 =1.732)
View Solutionस्पीति की समुद्र से ऊँचाई कितनी है,?
View Solutionएक जहाज 'A' 10 किमी/घं की चाल से पश्चिम दिशा की ओर गति कर रहा है। एक अन्य जहाज 'B इस जहाज A से 100 किमी दक्षिण दिशा में है और 10 किमी/घं की चाल से उत्तर दिशा की ओर जा रहा है। इन दोनों के बीच की दूरी कितने समय के पश्चात् न्यूनतम हो जायेगी?
View SolutionA starts walking at 4 kmph and after 4 hours, B starts cycling from the same point as that of A, in the same direction at 10 kmph. After how much distance from the starting point will B catch up with A (correct to two decimal places)?
A, 4 किमी/घंटा की चाल से चलना शुरू करता है और 4 घंटे के बाद, B, A के ही आरंभिक बिंदु से उसी दिशा में 10 किमी/घंटा की चाल से साइकिल चलाता है | आरंभिक बिंदु से कितनी दूरी ( दो दशमलव स्थान तक सही ) पर B, A को पकड़ लेगा?
View SolutionA train goes from P to Q with a speed ukm/h, then from Q to R (QR = 2PQ) with a speed 3 μ km/h, and returns from R to P with a speed μ/2km/h. What is the average speed (in km/h) of the train for the entire journey starting from P and back to P?
एक ट्रेन P से Q तक μ किमी/घंटा की चाल से जाती है तथा फिर Q से R तक ( QR = 2PQ) 3 μ/किमी/घंटा की चाल से जाती है और R से P तक μ/2 किमी/घंटा की चाल से वापस आती है | P से शुरू होकर P तक वापस आने के दौरान इस पूरी यात्रा में ट्रेन की औसत चाल ( किमी/घंटा में) ज्ञात करें |
View SolutionA person covers 40% of the distance from A to B at 8 km/h, 40% of the remaining distance at 9 km/h and the rest at 12 km/h. His average speed (in km/h) for the journey is :
एक व्यक्ति A से B तक की 40% दूरी 8 किमी/घंटा की चाल से, शेष दूरी का 40%, 9 किमी/घंटा की चाल से तथा शेष टूरी 12 किमी/घंटा की चाल से तय करता है | इस यात्रा में उसकी औसत चाल ( किमी/घंटा में ) कितनी रही है ?
View SolutionA man goes to a place on car at speed of 160 km/h and comes back at lower speed. If the average speed is 64 km/h in total, them the return speed (in km/h) is:
एक व्यक्ति कार से किसी स्थान को 160 किमी/घंटा की चाल से जाता है तथा कम चाल से वापस आता है | यदि कुल मिलाकर औसत चाल 64 किमी/घंटा है, तो वापसी की चाल (किमी/घंटा में ) है
View SolutionAmit travelled a distance of 50 km in 9 hours. He travelled partly on foot at 5km/h and partly by bicycle at 10km/h. The distance travelled on the bicycle is: /
अमित ने 9 घंटे में 50 किमी की दूरी तय की। उन्होंने आंशिक रूप से 5 किमी / घंटा की पैदल यात्रा की और आंशिक रूप से 10 किमी / घंटा की दर से साइकिल से यात्रा की। साइकिल पर तय की गई दूरी है:
View Solution
