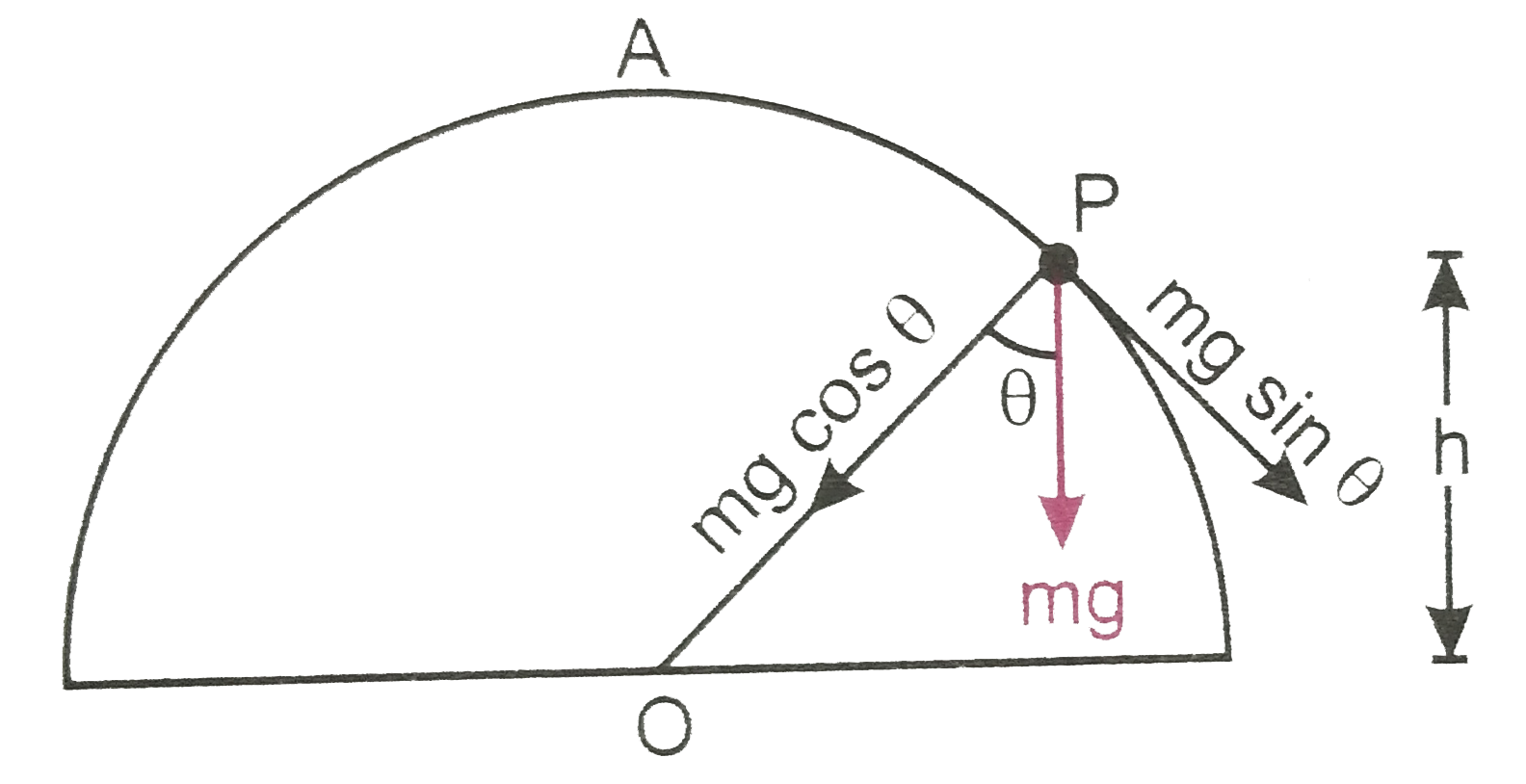
चित्र 6.14 में त्रिज्या R के एक चिकने अर्द्ध-गोले के उच्चतम बिंदु A पर एक चिकनी चकती राखी है जो कि इसके तल पर फिसलना प्रारा,बह करती है कितनी ऊंचाई पर चकती का अर्द्ध - गोले के तल से संपर्क हटेगा ?

माना चकती का संपर्क अर्द्ध-गोले के बिंदु P पर हटता है (चित्र 6.15) | बिंदु P पर स्पष्ट है कि चकती के भार mg का अर्द्ध-गोले के केंद्र की ओर अवयव mg cosθ,चकती पर लगने वाले अभिकेन्द्री बल के बराबर होगा अर्थात
mv2R=mg cosθ
अब यदि बिंदु P की ऊर्ध्वाधर ऊंचाई h है तो बिंदु A से P तक आने में चकती ऊर्ध्वाधर दूरी (R-h) तय करेगी तथा तब इसके द्वारा प्राप्त वेग v है तो
सूत्र v2=u2+2aS से,
v2=0+2g(R−h)=2g(R−h)
अतः समीकरण (i) व (ii) से,
2g(R−h)=g R cos θ
लेकिन cosθ=hR
∴ 2g(R−h)=gRhR=gh या h=23R
अर्थात ऊंचाई 23 पर चकती का अर्द्ध-गोले के तल से संपर्क हटेगा ।
Topper's Solved these Questions
- वृत्तीय गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - वृत्तीय गति EXERCISE - तथ्यात्मक प्रश्न
8 Videos
- वृत्तीय गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - वृत्तीय गति EXERCISE - वस्तुनिष्ठ प्रश्न (बताइए कि निम्न कथन सत्य है अथवा असत्य)
5 Videos
- मापन एवं मात्रक BOOK - SHIVLAAL PUBLICATIONCHAPTER - मापन एवं मात्रक EXERCISE - वस्तुनिष्ठ प्रश्न
67 Videos
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - वस्तुनिष्ठ प्रश्न
58 Videos
Similar Questions
एक वस्तु एकसमान कोणीय वेग से क्षैतिज वृत्त पर चल रही है बताइए कि निम्नलिखित में से कौन-सी राशियाँ नियत रहती है : रैखिक वेग, चाल, त्वरण, गतिज ऊर्जा, रैखिक संवेग ?
View Solutionएकसमान वृत्तीय गति में कण की गतिज ऊर्जा नियत रहती है ।
View SolutionS.I. पद्धति में कुल मूल मात्रको की संख्या है :
View Solutionनिम्नलिखित में से अदिश राशि है :
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionआर्गंड तल | आर्गंड तल पर सम्मिश्र संख्या के मापांक का ज्यामितीय अर्थ | एक सम्मिश्र संख्या का धुर्वीय निरूपण
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionआर्गंड तल | आर्गंड तल पर सम्मिश्र संख्या के मापांक का ज्यामितीय अर्थ | एक सम्मिश्र संख्या का धुर्वीय निरूपण
View SolutionBoards 2021|आइये जाने एक बिंदु से वृत पर स्पर्श रेखा के बारे में#!#वृत#!#Revision
View Solutionभूमिका |निर्देशांक तल #!#अंतरिक्ष में एक बिंदु के निर्देशांक#!#अष्टांश
View Solutionबिंदु L बिंदु P(3,4,5) से xz तल पर खींचे गए लंब का पाद बिंदु है | बिंदु L के निर्देशांक है
View Solutionअलग-अलग जगहों पर खड़िया-पट्टी के अलग-अलग नामों में से एक है
View Solutionएक कोण पर झुके हुए तल पर ऊँचाई से प्रक्षेप्य
View Solution
