(a) अन्योन्य प्रेरकत्व का अर्थ समझाइए । r1 तथा r2(r1<<r2) त्रिज्याओ की दो संकेन्द्री वृताकार कुण्डलियों पर विचार कीजिए जो समाक्ष स्थित हैं तथा जिनके केन्द्र संपाती हैं । इस व्यवस्था के लिए अन्योन्ये प्रेरकत्व के लिए व्यंजक प्राप्त कीजिए ।
(b) क्षेत्रफल A और फेरों की संख्या N की कोई आयताकार कुण्डली किसी एकसमान चुम्बकीय क्षेत्र B , जो कुण्डली के अभिलंबवत है , में 'f' चक्कर प्रति सेकण्ड से घूर्णन करायी जाती है। यह सिद्ध कीजिए की कुण्डली में प्रेरित अधिकतम emf का मान 2πfNBA है।
(a) अन्योन्य प्रेरकत्व -दो कुण्डलियों के बीच अन्योन्य प्रेरण गुणांक द्वितीयक कुण्डली में प्रेरित विधुत वाहक बल के बराबर होता है, जबकि प्रथमिक कुण्डली में धारा परिवर्तन की दर एंकाक हो।
दो सकेंद्रिय समतल वृताकार कुण्डलियो के बीच अन्योन्य प्रेरकत्व -माना दो समतल वृताकार कुण्डलिया जिनमे एक कम त्रिज्या r1 की तथा दूसरी अधिक त्रिज्या r2 की (r1<<r2) समाक्षीय रखी है तथा दोनों के केन्द्र सपाती है। माना त्रिज्या r2 वाली कुण्डली में फेरो की संख्या N2 तथा उसमे प्रवाहित धारा I2 है, तब कुण्डली के केन्द्र पर उत्पन चुम्बकीय क्षेत्र
B2=μ0N2I22r2
इस चुम्बकीय क्षेत्र को r1 त्रिज्या वाली कुण्डली के तल पर एकसमान माना जा सकता है क्योकि r1 अत्यंत अल्प है। यदि r1 त्रिज्या वाली कुण्डली में फेरो की संख्या N1 हो, तो इस कुण्डली से सम्ब्द्ध चुम्बकीय फ्लक्स
ϕ1=B2×N1×πr21
=μ0N1N2πr212r2I2
लेकिन परिभाषानुसार ,
ϕ1=MI2
अतः अन्योन्य प्रेरकत्व ,
M=μ0N1N22r2πr21 यही अभीष्ट व्यंजक है।
(b) माना क्षेत्रफल A और फेरो की संख्या N की कोई आयातकार कुण्डली एकसमान चुम्बकीय क्षेत्र B में f चक्कर प्रति सेकण्ड से घूर्णन करायी जाती है, अर्थात कोणीय वेग ω(2πf) से घूर्णन करायी जाती है। यदि प्रारम्भ में (t=0पर) कुण्डली का तल, चुम्बकीय क्षेत्र के लम्ब्वत है तथा समय t में घुमा गया कोण θ हो, तो समय t पर कुण्डली से सम्ब्द्ध चुम्बकीय फ्लक्स
ϕ=BANcosθ
=BANcosωt (∵θ=ωt)
तथा फैराडे के द्वितीय नियमनुसार , कुण्डली में प्रेरित वि. व. ब.
e=−dϕdt=BANomegsinωf
या e=2πfBANsin2πft ⟨.ω=2πf)
या e=e0sin2πft
जहा e0=2πfNBA कुण्डली में प्रेरित वि. वा. बल का अधिकतम मान है। अतः कुण्डली में प्रेरित अधिकतम वि. वा. बल
e0=2πfNBA
Topper's Solved these Questions
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विधुत-चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराएँEXERCISE - आंकिक प्रश्न11videos
विधुत-चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराएँ
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विधुत-चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराएँEXERCISE - सत्य/असत्य5videos
विधुत-चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराएँ
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विधुत-चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराएँEXERCISE - अति लघु उत्तरीय प्रश्न13videos
विधुत-चुम्बकीय प्रेरण एवं प्रत्यावर्ती धाराएँ
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विधुत-चुम्बकीय तरंगे EXERCISE - आंकिक प्रश्न3videos
विधुत-चुम्बकीय तरंगे
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - स्थिर विधुतिकी EXERCISE - आंकिक प्रश्न8videos
स्थिर विधुतिकी
Similar Questions
यदि किसी कुण्डली में धारा का मान 1 ऐम्पियर से शून्य तक 1 मिली सेकण्ड में घटने पर 4वोल्ट का विपरीत विधुत वाहक बल उत्पन होता है , तो कुण्डली के स्वप्रेरकत्व की गणना कीजिए ।
View Solutionसमान विभव की प्रत्यावर्ती धारा दिष्ट धारा से अधिक खतरनाक होती है।
05:10View Solutionचुम्ब्कीय फ्लक्स का S.I. मात्रक एवं विमीय सूत्र लिखिए ।
41:18View Solutionसोडियम लाइट की तरंगदैध्य्र 5890Å है।इसकी आवृति ज्ञात कीजिए । प्रकाश का वेग =3×108 मीटर / सेकण्ड ।
03:29View Solutionहीलियम के नाभिक के कारण उसमें 1Å की दूरी पर विघुत विभव की गणना कीजिए। हीलियम नाभिक पर आवेश =3.2×10−19 कुलॉम ।
49:49View Solutionवही मनुष्य है की जो मनुष्य के लिए मरे |
View Solutionअभिक्रिया (A+B)→उत्पाद के लिये निम्न आँकड़े प्राप्त हुए |
इन आँकड़ों से A एवं B के सन्दर्भ में अभिक्रिया की कोटि तथा सम्पूर्ण अभिक्रिया की कोटि का निर्धारण कीजिए। View Solution
View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
View Solutionपरिमेय संख्याओं 114 और −421 के लिए योग की क्रमविनिमेयता की जाँच कीजिए।
View Solutionस्व-प्रेरकत्व तथा अन्योन्य प्रेरकत्व में सम्बन्ध
View Solutionनए की जन्म कुण्डली : एक पाठ के रचनाकार कौन हैं ?
View Solutionकैप्रोलैक्टम में, यदि 'a', इलेक्ट्रॉनों (e^-) के एकाकी युग्मों की संख्या हैं तथा 'b', sp^3 संकरित परमाणुओं की संख्या हैं। a + b का मान क्या है?
View Solutionनिम्न के लिए हाइड्रोजनीकरण की ऊष्मा की तुलना कीजिए-
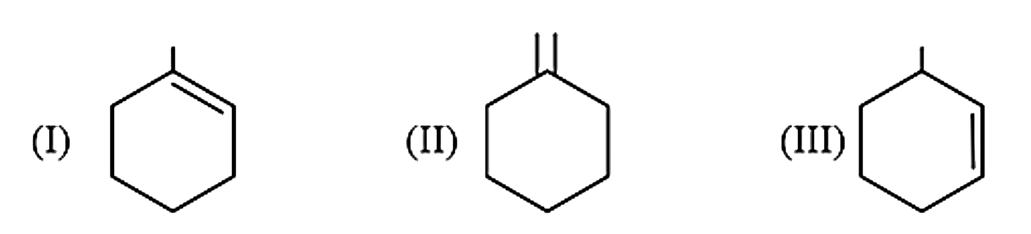 36:52View Solution
36:52View Solutionजब N2 का 80% N2O3 में परिवर्तित होता है तो N2 ,7g के साथ संयोजन के लिए आवश्यक ऑक्सीजन परमाणुओं की संख्या की गणना कीजिए।
39:43View SolutionCr परमाणु (Z = 24) की मूल अवस्था पर विचार कीजिए। द्विगंशी क्वान्टम संख्या, I = 1 और 2 के साथ इलेक्ट्रॉनों की संख्या क्रमश: हैं:
00:59View Solutionनिम्नलिखित अभिक्रिया के लिए अभिक्रिया की ऊष्मा की गणना कीजिए: SO_(2) +(1)/(2)O_(2) to SO_(3) SO_(2) और SO_(3) के निर्माण की ऊष्मा के मान - 298.2 kJ और -98.2 kJ दिए गए हैं।
01:14View Solution

