एक R त्रिज्या की पतली वलय पर Q आवेश एक समान रूप से वितरित है वलय की अक्ष पर केन्द्र से X दूरी पर स्थित बिन्दु विधुत क्षेत्र की तीव्रता ज्ञात कीजिए। प्राप्त परिणाम की प्रतिबंध x>>R के लिए विवेचना कीजिए।
वलय पर आवेश (q) एकसमान रूप से वितारित है अत: रेखीय घनत्व
λ=QL=q2πR
हम वलय पर व्यासत: सम्मुख दो समान लम्बाइ। dl के अल्पांश A तथा B लेते है। प्रत्येक अल्पांश पर आवेश की मात्रा
dq=λdl
प्रत्येक अल्पाश से बिन्दु P की दूरी r है तो अल्पांश A के कारण बिन्दु P पर विधुत क्षेत्र
dE1=14πε0.dqr2
अल्पांश B के कारण बिन्दु P पर विधुत क्षेत्र dE2=14πε0.dqr2
|dE1|=|dE2|
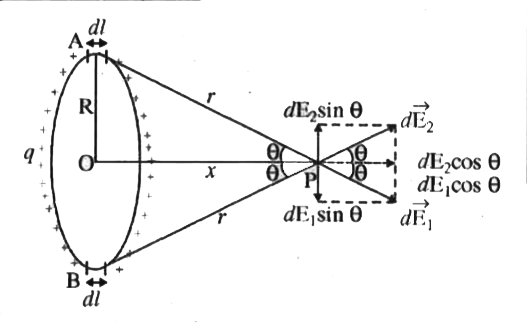
dE1 एवं dE2 को चित्रानुसार वियोजित करने पर इनके ऊर्ध्वघटक dE1sinθ एवं dE2sinθ परिमाण में समान परस्पर विपरीन होने के कारण परस्पर निरस्त हो जाते है। जबकि क्षेतिज घटक dE1cosθ एवं dE2cosθ समान दिशा में होने के कारण जुड जाते है। हम समपूर्ण वलय को इसी का क्षैतिज घटक OP दिशा के अनुदिश होता है। अत: सम्पूर्ण वलय के कारण बिन्दु P पर विघुत क्षेत्र
E=∫L.dEcosθ=14πε0∫L.dqr2cosθ
∴ चित्र से cosθ=xr,:’,dq=λdl तथा x,λ एवं r नियतांक है।
अत: समीकरण (1) से
E=14πε0∫Lλdlr2×xr
⇒E=λx4πε0∫Ldl
∫Ldl= सम्पूर्ण वलय की लम्बाई =2πR
अत: E=λx4πε0r3×2πR
∴,λ×2πR=q तथा चित्र से r2=R2+x2
प्रतिबंधx>>R के लिए उपरोक्त सूत्र
E=kqx(x2)32(R2x2+1)32
यहाँ x>>R
∴,R2x2=0 लेने पर
अत: E=kqxx3(0+1)3/2=kqxx2=kqx2
E=kqx2
यह सूत्र किसी बिन्दु आवेश Q से x दूरी पर स्थित बिन्दु पर विधुत क्षेत्र के सूत्र के समान ही है। अत, अक्ष पर दूरस्थ बिन्दुओं के लिए वलय इस प्रकार व्यवहार करती है। मानों सम्पूर्ण आवेश इसके केन्दु पर संकेन्द्रित हे।
Topper's Solved these Questions
- गाउस का नियम एव इसके अनुप्रयोग BOOK - SANJEEV PUBLICATIONCHAPTER - गाउस का नियम एव इसके अनुप्रयोग EXERCISE - वस्तुनिष्ठ प्रश्न-
26 Videos
- गाउस का नियम एव इसके अनुप्रयोग BOOK - SANJEEV PUBLICATIONCHAPTER - गाउस का नियम एव इसके अनुप्रयोग EXERCISE - अतिलघुत्तरात्मक प्रश्न-
19 Videos
- किरण प्रकाशिकी BOOK - SANJEEV PUBLICATIONCHAPTER - किरण प्रकाशिकी EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (उच्च स्तरीय बुद्धि-कौशल प्रश्न )-
9 Videos
- चुम्बकत्व एवं चुम्बकीय पदार्थो के गुणBOOK - SANJEEV PUBLICATIONCHAPTER - चुम्बकत्व एवं चुम्बकीय पदार्थो के गुणEXERCISE - अन्य महत्त्वपूर्ण प्रश्न(उच्चस्तरीय बुद्धि-कौशल प्रश्न)
27 Videos
Similar Questions
विघुत क्षेत्र की तीव्रता →E को वैधुत बल रेखाओं द्वारा भी निरूपित किया जाता है। जहाँ पर E का मान होगा-
View Solutionवैधुत फलक्स को परिभाषित कीजिए। इसका S.I मात्रक लिखिए।
View Solutionनिम्नलिखित प्रश्न ों के उत्तर लिखिए-
(a) निम्न चित्र में अपवर्तनांक 1.68 के तंतु से बानी किसी प्रकाश नलिका (लाइट पाइप) का अनुप्रस्थ परिछेद दर्शाया गया है| नलिका का बाह्म आवरण 1.44 अपवर्तनांक के पदार्थ का बना है| नलिका के अक्ष से आपतित किरणों के कोणों का परिसर, जिनके लिए चित्र में दर्शाए अनुसार नलिका के भीतर पूर्ण परावर्तन होते है, ज्ञात कीजिए|
(b) यदि पाइप पर बाह्म आवरण न हो तो क्या उत्तर होगा?

View Solutionकिसी चुम्बक (द्विध्रुव) के उत्तरी (या दक्षिणी) ध्रुव से परिणामी चुम्बकीय फ्लक्स क्या है?
View Solutionपृथ्वी की त्रिज्या 6.4×106 मी है। पृथ्वी-तल से 800 किमी की ऊँचाई पर गुरुत्वीय विभव तथा गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए। (g=10 मी/से.2)
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।
View Solutionआवेशित वलय के कारण विद्युत क्षेत्र की तीव्रता
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionवलय के अक्ष पर स्थित बिंदु पर विधुत क्षेत्र की तीव्रता
View Solutionसरल रेखाएँ|एक बिन्दु की रेखा से दूरी#!#दो समांतर रेखाओ के बीच की दूरी#!#प्रश्नो पर चर्चा
View Solutionधरावाही वलय के अक्ष पर चुंबकीय क्षेत्र
View Solution
