C धारिता वाले अनेक सधारित्र चित्र में दर्शाये अनुसार अनंत संख्या में संयोजित है | बिंदु A और B के मध्य कुल धारिता का मान ज्ञात कीजिये |
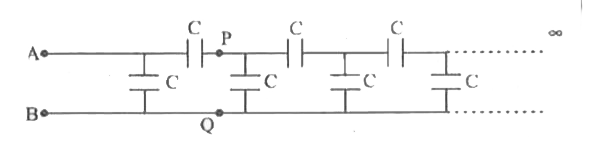
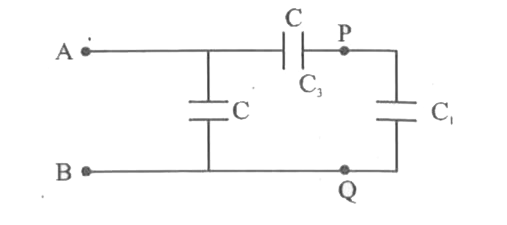
चूँकि चित्र में श्रेणी अनंत लम्बाई की है , अतः बिंदुओं होगा जो की श्रेणी के बिंदुओं A व् B के दाहिनी और है | यदि श्रेणी की तुल्य धारिता C1 हो तो दिए गये चित्र के संयोजन को नए चित्र द्वारा प्रतिस्थापित कर सकते है |
अतः A व् B के मध्य तुल्य धारिता
C1=C+CC1C+C1
C1=C(C+C1)+CC1(C+C1)
या C1C+C21=C2+CC1+CC1
C21−CC1−C2=0
यह समीकरण C1 में दीघाट समीकरण है |
C1=C±√C2+4C22=C±√5C22
C1=C+√5C2=C2(1−+√5)
अर्थात C1=(1+√5)C2 या C1=(1−√5)C2
∵ धारिता का मान सदैव घनात्मक होता है अतः दिए गये संयोजन की तुल्य धारिता
C1=(1+√5)C2 होगी |
Topper's Solved these Questions
- विधुत धारिता BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत धारिता EXERCISE - वस्तुनिष्ठ प्रश्न---
26 Videos
- विधुत धारिता BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत धारिता EXERCISE - अतिलघुत्तरामक प्रश्न---
29 Videos
- विधुत क्षेत्र BOOK - SANJEEV PUBLICATIONCHAPTER - विधुत क्षेत्र EXERCISE - अन्य महत्तवपूर्ण प्रश्न
54 Videos
Similar Questions
विभवांतर V, आवेश Q तथा धारिता C में सम्बन्ध है--
View Solutionविधुत का सबसे अच्छा चालक कोनसा है ?
View Solutionकिसी विद्युत द्विध्रुव के निरक्षीय रेखा पर स्थित बिंदु पर विद्युत क्षेत्र की दिशा क्या होती है?
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
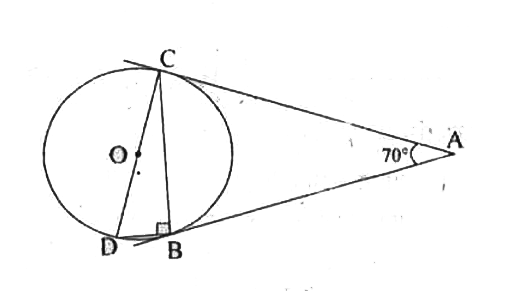
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionचित्र में दिया गया वृत्त चार्ट मई -जून 2013 के दौरान वाहनों का केन्द्र्य सर्कार द्वारा चल्या गये अभियान में कटे हुए चलानो की संख्या को डिग्री (∘ ) में दर्शाता है। इसे ध्यानपूर्वक पढ़िए व निम्न प्रशनो के उत्तर दीजिए।
यदि कुल वाहनों 72 लाख है तो मध्य प्रदेश में कटे चालानों की संख्या राजस्थान के कटे चालानों की संख्या से कितना अधिक है ?

View Solutionचित्र में दिया गया वृत्त चार्ट मई -जून 2013 के दौरान वाहनों का केन्द्र्य सर्कार द्वारा चल्या गये अभियान में कटे हुए चलानो की संख्या को डिग्री (∘ ) में दर्शाता है। इसे ध्यानपूर्वक पढ़िए व निम्न प्रशनो के उत्तर दीजिए।
यदि कुल वाहनों 72 लाख है तो मध्य प्रदेश में कटे चालानों की संख्या राजस्थान के कटे चालानों की संख्या से कितना अधिक है ?

View Solutionनिम्नलिखित में से कौन-सी संख्या 27 और 97 के मध्य में नहीं हैं :
View Solutionकिस अनुपात में बिंदु (−25,a) बिंदुओं (-4,3) और (2,8) को विभाजित करता है ? a का मान ज्ञात कीजिए।
View Solutionधारिता |आयतन एवं धारिता में अन्तर
View SolutionRecap|चालक की धारिता |गोलीय चालक की धारिता |धारिता को प्रभावित करने वाले कारक |संधारित्र का सिद्धांत |OMR|Summary
View Solutionमिश्रण का तापमान #!#गुप्त ऊष्मा धारिता #!#अवस्था में परिवर्तन के लिए आवश्यक ऊष्मा
View Solutionतापमान व समय के मध्य ग्राफ #!#ऊष्मा का जल तुल्यांक #!#ऊष्मा धारिता व बर्फ को जमने में लगा समय
View SolutionThe sum of a number and its reciprocal is 174 . Find the numbers.
एक संख्या और उसकी परस्पर संख्या का जोड़ 174 है| संख्या का मान ज्ञात कीजिये |
View Solutionधारिता|संधारित्र का सिद्धांत|आवेशित संधारित्र में संचित ऊर्जा|गोलीय संधारित्र की धारिता|OMR|Summary
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
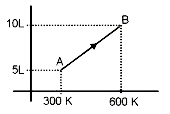
View Solution
