सिद्ध कीजिए की एक ही आधार पर व समान्तर रेखाओं के एक युग्म के बीच स्थित त्रिभुज क्षेत्रफल में बराबर (समान) होते है ।
और एक ही आधार पर तथा एक ही समांतर रेखाओं तथा के बीच स्थित हैं।
सिद्ध करना है:
रचना: || तथा || खींचा।
##image##
प्रमाण: एक समांतर चतुर्भुज है। तथा भी एक समांतर चतुर्भुज है।
चूँकि समांतर चतुर्भुज तथा समांतर चतुर्भुज FBCD एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित हैं।
....
लेकिन समांतर चतुर्भुज का विकर्ण है
....
इसी प्रकार हम साबित कर सकते हैं कि
....
, तथा से
यही सिद्ध करना था।
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:SHIVLAAL PUBLICATIONChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:दीर्घ उत्तरीय प्रश्न
Explore 3 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:SHIVLAAL PUBLICATIONChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:अति लघु उत्तरीय प्रश्न
Explore 3 Videos
- रेखाएँ और कोण Book:SHIVLAAL PUBLICATIONChapter:रेखाएँ और कोण Exercise:दीर्घ उत्तरीय प्रश्न
Explore 4 Videos
- सांख्यिकी Book:SHIVLAAL PUBLICATIONChapter:सांख्यिकी Exercise:लघु उत्तरीय प्रश्न
Explore 8 Videos
Similar Questions
दर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफल वाले चार त्रिभुजों में बाँटते हैं।
View Solutionकिस समान्तर चतुर्भुज का आधार 20 सेमी तथा ऊँचाई (शीर्षलम्ब) 10 सेमी है, तो समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए ।
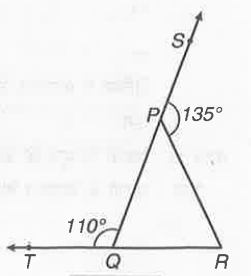
View Solutionसंलग्न चित्र में ΔPQR की भुजाओं QP और RQ को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है। यदि ∠SPR=135∘ और ∠PQT=110∘ है, तो ∠PRQ ज्ञात कीजिए।
View Solutionआठवीं कक्षा के 30 विधार्थियो के रक्त समूह ये हैं :
A,B,O,O,AB,O,A,O,B,A,O,B,A,O,O,A,AB,O,A,A,O,O,AB,B,A,O,B,A,B,O.
इन आँकड़ो को एक बारम्बारता बंटन सारणी के रूप में प्रस्तुत कीजिए । बताइए की इन विधार्थियो में कौन सा रक्त समूह अधिक समान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है ?
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionअथवा 'कारतूस' पाठ के आधार पर सोदाहरण सिद्ध कीजिए कि वज़ीर अली एक जांबाज़ सिपाही था।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |एक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|NCERT प्रश्नावली|सारांश
View Solutionसमांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल |एक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|अभ्यास कार्य|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज|प्रमेय|अभ्यास कार्य|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solutionएक ही आधार पर और एक ही समांतर रेखाओं के बीच आकृतियाँ|प्रमेय|NCERT प्रश्नावली|सारांश
View Solution
