R त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृत्ति ω से घूर्णन कर रहा है | यह दर्शाइए कि इस तार में डाली कोई मणिका ω≤√g/R के लिए अपने निम्नतम बिंदु पर रहती है | ω=√2g/R के लिए , केंद्र से मनके को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है | ( घर्षण को उपेक्षणीय मानिए | )
मानलो जब मनिका कोणीय आवृत्ति ω से घूर्णन करती है , तो उसकी स्थिति P है P को केंद्र O से मिलाने वाली त्रिज्यीय रेखा ऊर्ध्वाधर सेθ कोण बनाती है | तब मनिका पर अभिलंब प्रतिक्रिया N, OP के अनुदिश कार्य करेगी | N को दो घटकों में वियोजित किया जा सकता है -
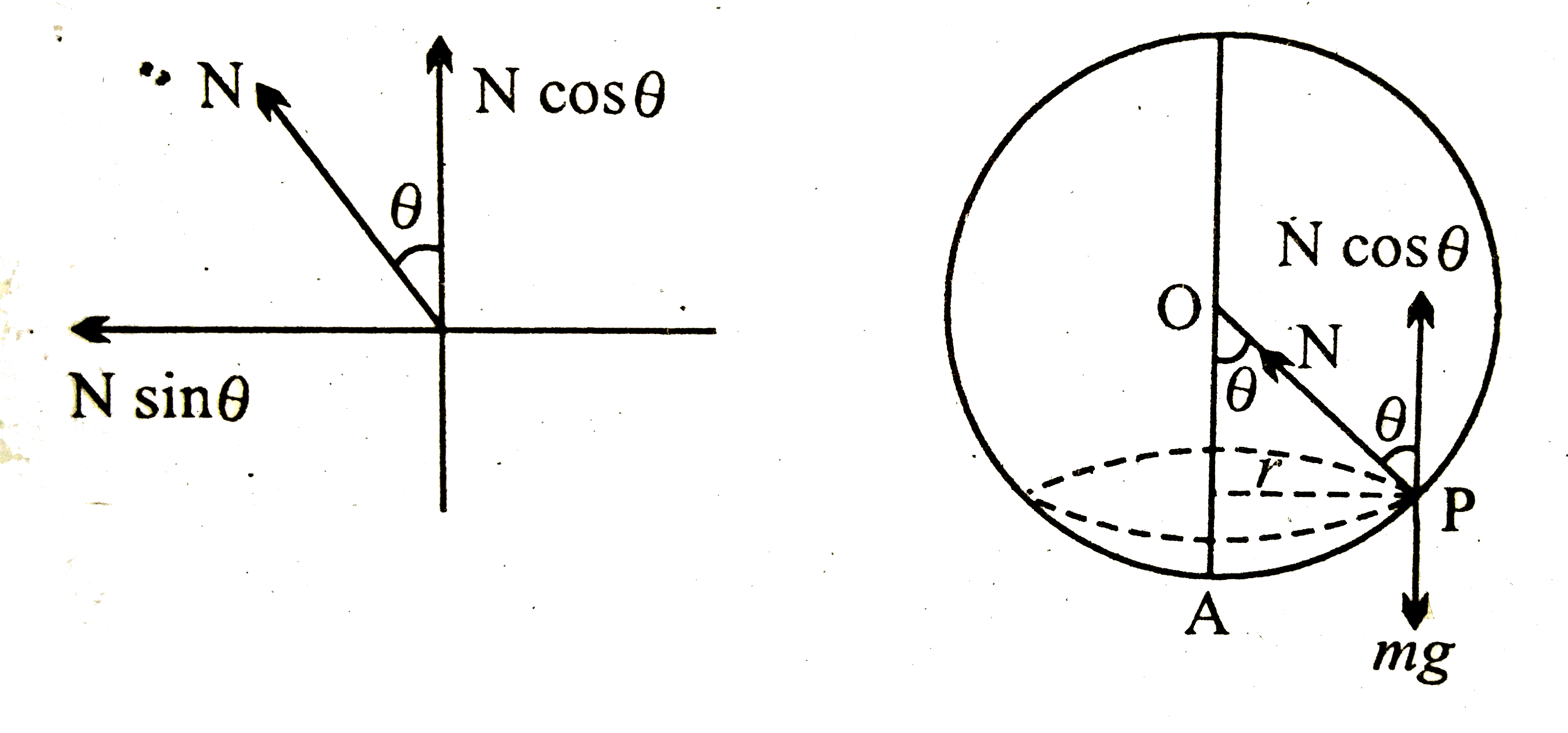
(i) Ncosθ ऊर्ध्वाधर ऊपर की ओर , जो मनिका के भार mg को संतुलित करता है , जहाँ m मनिका की संहति है |
(ii) Nsinθ क्षैतिज दिशा में , जो मनिका को क्षैतिज तल में वृत्तीय गति करने के लिए अभिकेंद्र बल प्रदान करता है |
इस प्रकार, Ncosθ=mg ..(1)
तथा Nsinθ=mrω2
किन्तु r=Rsinθ, जहाँ R वृत्तीय तार की त्रिज्या है (PO = R)
∴ Nsinθ=mRsinθ.ω2 या N=mRω2
समी (1 ) में मान रखने पर,
mRω2cosθ=mg
या cosθ=gRω2 ...(2)
मणिका को निम्नतम बिंदु A पर रहने के लिए θ∘=0
∴ cosθ=1
समी. (2 ) में मान रखने पर,
gRω2=1
या ω=√gR
यदि ω>√gR हो, तो मणिका न्यूनतम बिंदु A से ऊपर उठेगा । अतः मणिका को निम्नतम बिंदु पर रहने के लिए
ω≤√gR
पुनः यदि ω=√2gR हो, तो समी. (2 ) से,
cosθ=gR×R2g=12
∴ θ=60∘.
Topper's Solved these Questions
- एकसमान वृत्तीय (वर्तुल) गति की गतिकी BOOK - NAVBODHCHAPTER - एकसमान वृत्तीय (वर्तुल) गति की गतिकी EXERCISE - बहुविकल्पीय प्रश्न
37 Videos
- ऊष्मागतिकी BOOK - NAVBODHCHAPTER - ऊष्मागतिकी EXERCISE - NCERT पाठ्य पुस्तक के प्रश्नोत्तर
16 Videos
- कणों के निकाय की गति और घुर्णो गति BOOK - NAVBODHCHAPTER - कणों के निकाय की गति और घुर्णो गति EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
50 Videos
Similar Questions
150 मीटर त्रिज्या तथा 0.6 घर्षण गुणांक वाले वक्राकार मार्ग को पार करते समय एक कार ड्राइवर को किस अधिकतम चाल ( मी/से ) से कार को चलाना चाहिए जिससे कि वह फिसले नहीं -
View Solutionकोई गीजर 3.0 लीटर प्रति मिनट की दर से बहते हुए जल को 27∘Cतक 77∘Cगर्म करता है | यदि गीजर का परिचालन गैस बर्नर द्वारा किया जाये तो ईंधन के व्यय की क्या दर होगी ? बर्नर के ईंधन की दहन -ऊष्मा 4.0×104J g−1 है ?
View Solutionएकसमान द्रव्यमान घनत्व के निम्नलिखित पिंडों में प्रत्येक के द्रव्यमान केंद्र की अवस्थिति लिखिए-
( a ) गोला, ( b ) सिलिंडर, ( c ) छल्ला तथा ( d ) घन ।
क्या किसी पिंड का द्रव्यमान केंद्र आवश्यक रूप से उस पिंड के भीतर स्थित होता है ?
View Solutionदरअसल शुरू से ही था हमारे आदेशों में कही एक जानी दुश्मन कि घर को बचाना है लूटेरों से शहर को बचाना है नदियों से देश को बचाना है , देश के दुश्मनों से बचाना है - नदियों को नाला हो जाने से हवा को धुआँ हो जाने से खाने को जहर हो जाने से : बचाना है - जंगल को मरुस्थल हो जाने से , बचाना है - मनुष्य को , जंगल हो जाने से । उपर्युक्त पद्यांश का भावार्थ अपने शब्दों में लगभग ६ से ८ पक्तियों में लीखिए ।
View Solutionनिम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए
शांभा- "हमारे प्यारे सरपंच के हुकम से इस कंजूस किरोड़ीमल को सजा दी जाती है कि यह उसी लड़की से जाकर अपने लड़के की शादी कम व्यय में करे। अपने समधी से माफी माँगे।
किरोड़ीमल को सजा कौन देता है ?
View Solutionनिम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए शांभा- "हमारे प्यारे सरपंच के हुकम से इस कंजूस किरोड़ीमल को सजा दी जाती है कि यह उसी लड़की से जाकर अपने लड़के की शादी कम व्यय में करे। अपने समधी से माफी माँगे। किरोड़ीमल को किससे क्षमा माँगने के लिए कहा गया है ?
View Solutionनिम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए शांभा- "हमारे प्यारे सरपंच के हुकम से इस कंजूस किरोड़ीमल को सजा दी जाती है कि यह उसी लड़की से जाकर अपने लड़के की शादी कम व्यय में करे। अपने समधी से माफी माँगे। उपयुक्त अवतरण में किस समस्या पर प्रकाश डाला गया है ?
View Solutionएक चुंबकीय सुई को, जो चुंबकीय क्षेत्र के अनुदिश है, क्षेत्र से 60∘ के कोण पर घुमाने के लिए W इकाई कार्य करना पड़ता है। सुई को इस स्थिति में रखने के लिए आवश्यक बल आघूर्ण का मान ज्ञात कीजिए।
View Solutionनिम्नलिखित व्यंजकों में से कौन-कौन से बहुपद है | अपने उत्तर के लिए कारण लिखिए :
3√x+x2
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View SolutionM, N, P, R, T, W, F and H are sitting around a circle at the centre, P is third to the left of M and second to the right of T. N is second to the right of P. R is second to the right of W who is second to the right of M. F is not an immediate neighbour of P. Who is to the immediate right of P?
M, N, P, R, T, W, F और H केंद्र में एक वृत्त के चारों ओर बैठे हैं,P, M के बाएं से तीसरे और T के दायें से दूसरे स्थान पर हैं| N, Pके दाईंओर दूसरा है। R, W के दायें से दूसरे नंबर पर है, जो M के दायें से दूसरे नंबर पर है, P का तत्काल पड़ोसी नहीं है। P के तत्काल दाएं को कौन है?
View SolutionIf '+' stands for'+', '-' stands for '=', 'x' stands for '+', '+' stands for greater than, '=' stands for less then, '>' stands for multiplication and '<' stands for subtraction, then which of the following alternatives is correct?
View Solutionनिम्नलिखित में से अभिकारकों के किस समूह का उपयोग फेनोल से पेरासिटामोल के निर्माण के लिए किया जाता है
View Solutionएक एंजाइम उत्प्रेरित अभिक्रिया के लिए, ताप (T) के सापेक्ष अभिक्रिया की दर (r) को आलेखित किया गया है। निम्नलिखित में से कौन सा सही निरूपण है?
View Solutionनिम्नलिखित में से कौन CO के लिए एक सिंक है?
View Solutionऐसीटैमाइड को मेथेनेमीन में परिवर्तित करने के लिए निम्नलिखित में से कौन सी अभिक्रिया उपयुक्त है?
View Solution
