कणों के किसी निकाय की गति को इसके द्रव्यमान केंद्र की गति और द्रव्यमान केंद्र के पारित : गति में अलग - अलग करके विचार करना दर्शाइए कि-
(d)
यह भी दर्शाइए कि
( जहाँ द्रव्यमान केंद्र के परितः निकाय पर लगाने वाले सभी बाह्य बल आघूर्ण हैं । )
( संकेत - द्रव्यमान केंद्र की परिभाषा एवं न्यूटन के गति के तृतीय नियम का उपयोग कीजिए । यह मान लीजिए कि किन्हीं दो कणों के बीच के आतंरिक बल उनको मिलाने वाली रेखा के अनुदिश कार्य करते हैं ।)
चित्र में O किसी निर्देश तंत्र का मूलबिंदु, C कणों के द्रव्यमान केंद्र की स्थिति तथा द्रव्यमान वाले - वें कण की स्थिति है ।
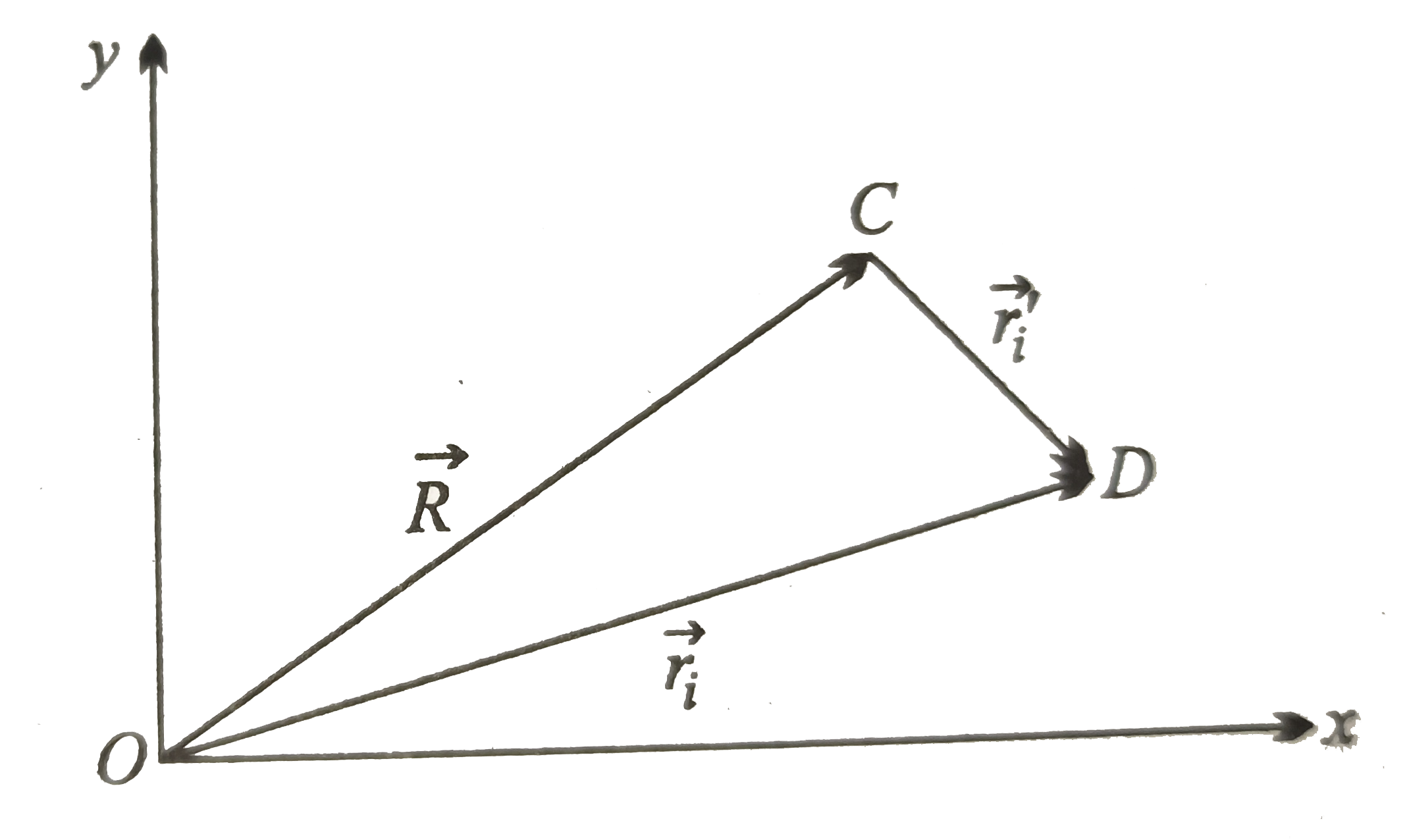
मानलो द्रव्यमान केंद्र का स्थिति सदिश तथा - वें कण का स्थिति सदिश है । द्रव्यमान केंद्र का वेग तथा - वें कण का वेग है ।
किन्तु
या यही सिद्ध करना था।
Topper's Solved these Questions
- कणों के निकाय की गति और घुर्णो गति BOOK - NAVBODHCHAPTER - कणों के निकाय की गति और घुर्णो गति EXERCISE - बहुविकल्पीय प्रश्न
84 Videos
- एकसमान वृत्तीय (वर्तुल) गति की गतिकी BOOK - NAVBODHCHAPTER - एकसमान वृत्तीय (वर्तुल) गति की गतिकी EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
60 Videos
- कार्य, ऊर्जा और शक्ति BOOK - NAVBODHCHAPTER - कार्य, ऊर्जा और शक्ति EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
51 Videos
Similar Questions
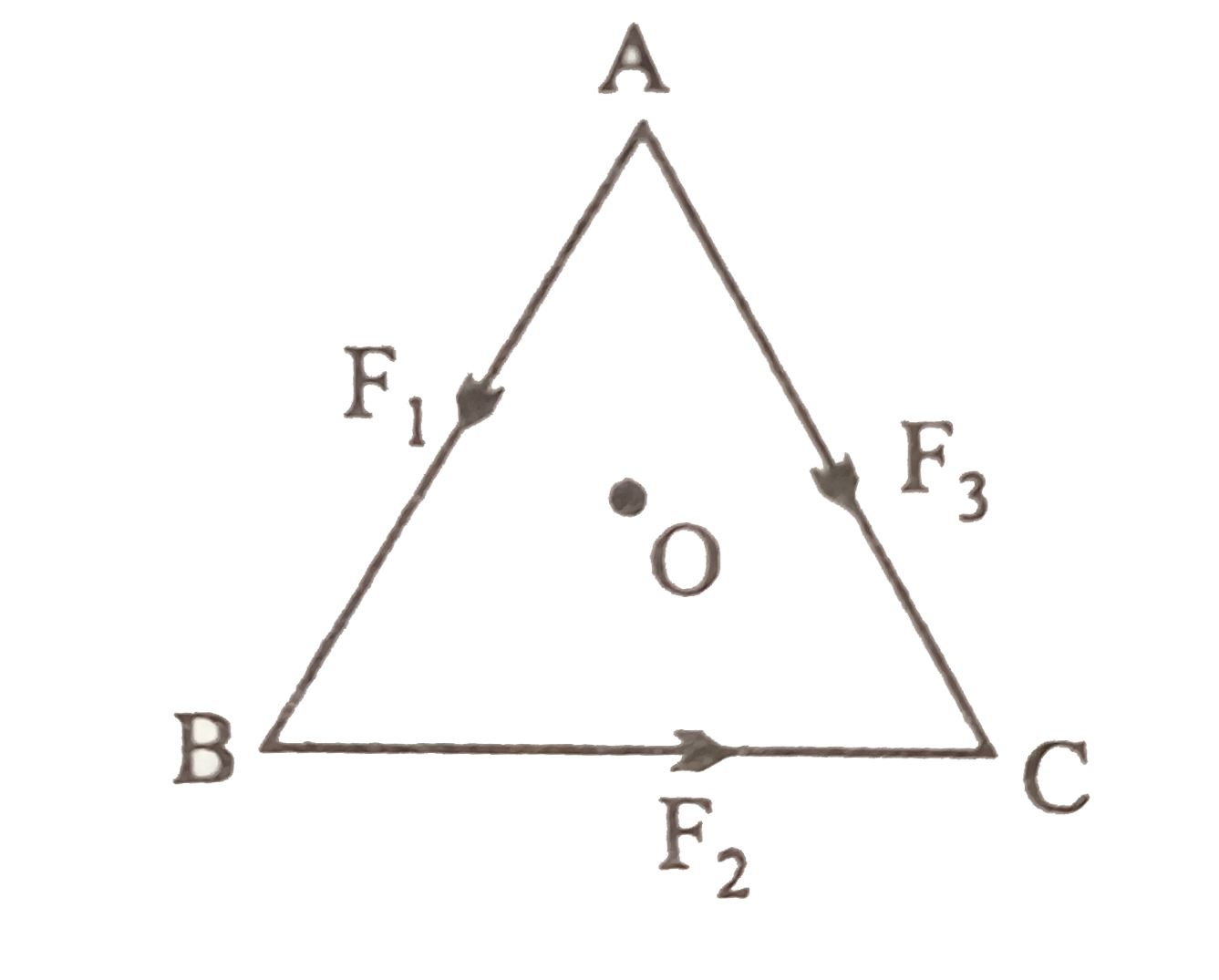
एक समबाहु त्रिभुज ABC का केंद्र O है । F1,F2 और F3 क्रमशः AB, BC व AC के अनुदिश कार्यरत बल हैं । F3 का मान क्या होगा जबकि O के परितः कुल बल - आघूर्ण शून्य है ।
View Solutionनिम्नलिखित पर कार्यरत नेट बल का परिमाण व उसकी दिशा लिखिए -
( a ) एकसमान चाल से नीचे गिरती वर्षा की कोई बूँद
View Solutionकिसी वस्तु पर किसी बल द्वारा किए गए कार्य का चिह्व समझना महत्वपूर्ण है । सावधानीपूर्वक बताइए कि निम्न लिखित राशियाँ धनात्मक हैं या ऋणात्मक-
( a ) किसी व्यक्ति द्वारा किसी कुँए में से रस्सी से बँधी बाल्टी को रस्सी द्वारा बाहर निकालने में किया गया कार्य ।
View Solutionद्रव्यमान केंद्र की गति व कणो के निकाय का रेखीय संवेग
View Solutionविभिन्न वस्तुओं का द्रव्यमान केंद्र।द्रव्यमान केंद्र की गति व कणो के निकाय का रेखीय संवेग
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionखंडित वस्तुओं का द्रव्यमान केंद्र |द्रव्यमान केंद्र की गति
View Solutionद्रव्यमान केंद्र की गति
View Solutionद्रव्यमान केंद्र की गति
View Solutionद्रव्यमान केंद्र की गति#!#द्रव्यमान केंद्र ज्ञात करना
View Solutionपृथ्वी के गुरुत्वीय बल के प्रभाव में वस्तुओ की गति |प्रश्न |द्रव्यमान |OMR|Summary
View Solutionप्रस्तावना#!#द्रव्यमान केंद्र#!#घूर्णी गति
View Solutionn कणों के निकाय के द्रव्यमान का केंद्र#!#अभ्यास प्रश्न
View Solutionद्रव्यमान केंद्र की गति
View Solutionद्रव्यमान केंद्र|विविक्त कणों के निकाय का द्रव्यमान केंद्र|विभिन्न कणों के निकाय का द्रव्यमान केंद्र|सतत वितरण वाले द्रव्यमान का द्रव्यमान केंद्र|द्रव्यमान केंद्र की गति|OMR|Summary
View Solutionद्रव्यमान केंद्र |विवित्तक कणो के नियम के लिए द्रव्यमान केंद्र |OMR
View Solution
