समान द्रव्यमान m के तीन बिंदु द्रव्यमान l भुजा वाले एक समबाहु त्रिभुज के शीर्ष पर स्थित हैं । इसके केंद्र ( Centroid ) पर गुरुत्वीय क्षेत्र एवं विभव का मान ज्ञात कीजिए ।

Video Solution

Text Solution

Verified by Experts

चित्र में ABC एक समबाहु $Δ$ है ।

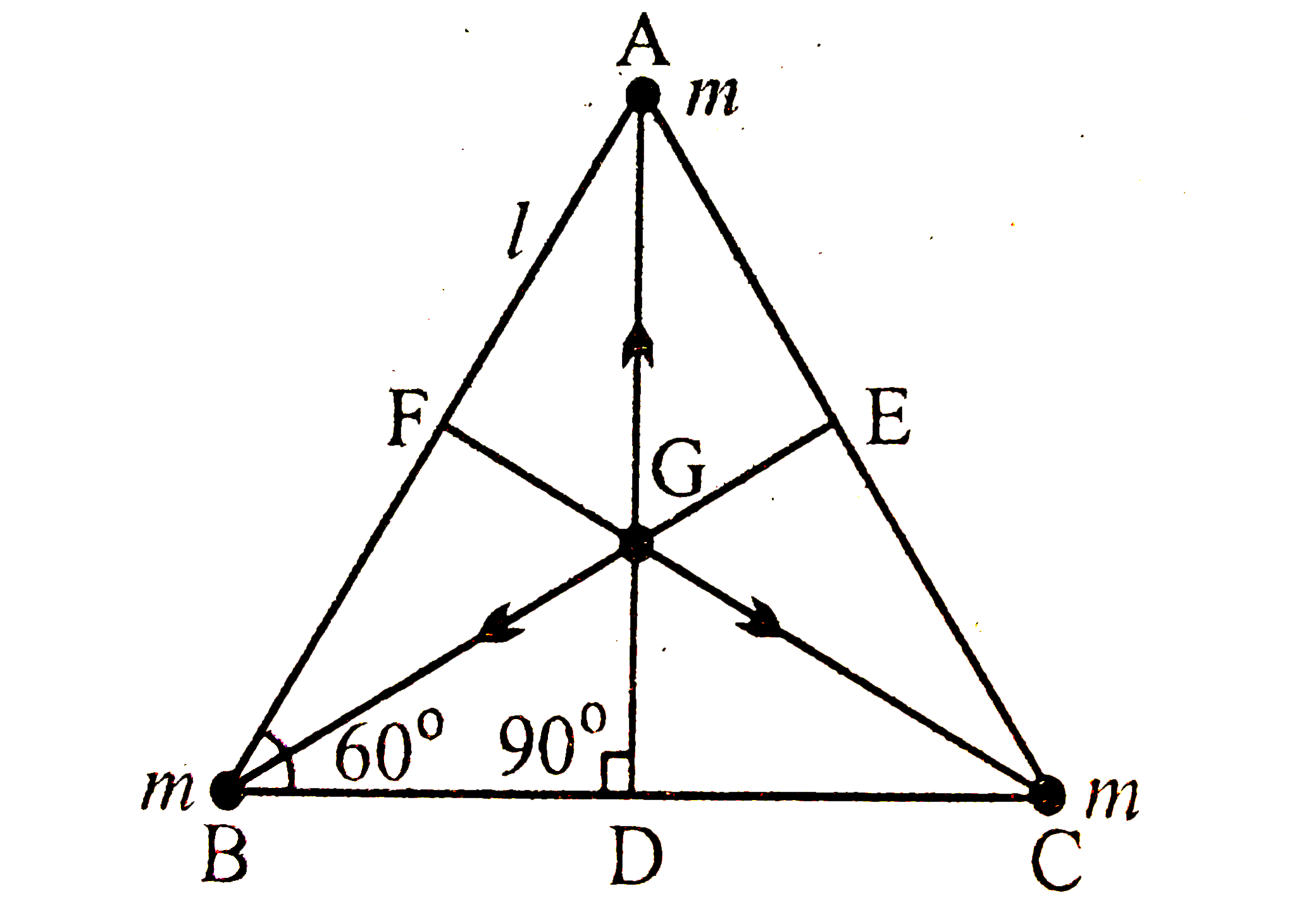
G उसका केंद्र है।
समकोण $Δ A D B$ में,
${sin 60}^{\circ} = \frac{A D}{A B} \Rightarrow \frac{\sqrt{3}}{2} = \frac{A D}{l} \Rightarrow A D = \frac{\sqrt{3} l}{2}$
किन्तु $A G = \frac{2}{3} A D r A R r A G = \frac{2}{3} \times \frac{\sqrt{3} l}{2} = \frac{l}{\sqrt{3}}$
इसी तरह $B G = \frac{1}{\sqrt{3}}$ तथा $C G = \frac{l}{\sqrt{3}}$
अतः $A G = B G = C G = \frac{l}{\sqrt{3}}$
बिंदु A पर स्थित बिंदु द्रव्यमान m के कारण G पर गुरुत्वीय क्षेत्र $E_{A} = \frac{G m}{A G^{2}}$
बिंदु B पर स्थित बिंदु द्रव्यमान m के कारण G पर गुरुत्वीय क्षेत्र $E_{B} = \frac{G m}{B G^{2}}$
बिंदु C पर स्थित बिंदु द्रव्यमान m के कारण G पर गुरुत्वीय क्षेत्र $E_{C} = \frac{G m}{C G^{2}}$
अतः $E_{A} = E_{B} = E_{C} = E$ (मानलो)
तीनों बलों के बीच का परिणामी का परिमाण तीसरे बल के परिमाण के बराबर है।
अतः केंद्र G पर गुरुत्वीय क्षेत्र का मान शून्य होगा। अब बिंदु पर गुरुत्वीय विभव
$= - \frac{G m}{A G} + (- \frac{G m}{B G}) + (- \frac{G M}{C G})$
$= - G M [\frac{1}{A G} + \frac{1}{B G} + \frac{1}{C G}]$
$= - G M [\frac{\sqrt{3}}{l} + \frac{\sqrt{3}}{l} + \frac{\sqrt{3}}{l}]$
$= - 3 \sqrt{3} \frac{G M}{l} .$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

NAVBODH-गुरुत्वाकर्षण -आंकिक उदाहरण प्लस

Home
Ask Doubt
Profile