और द्रव्यमान के दो पिंड d दूरी पर स्थित हैं । सिद्ध कीजिए कि उस स्थिति में , जहाँ पर उनके कारण गुरुत्वीय क्षेत्र शून्य है , विभव निम्न समीकरण द्वारा दिया जाता है -
.
मानलो द्रव्यमान के पिंड से x दुरी पर उनके बीच गुरुत्वीय क्षेत्र शून्य है। तब,
या
अतः इस स्थिति में दोनों पिंडों के कारण विभव,
Topper's Solved these Questions
- गुरुत्वाकर्षण BOOK - NAVBODHCHAPTER - गुरुत्वाकर्षण EXERCISE - बोधात्मक प्रश्न
4 Videos
- गुरुत्वाकर्षण BOOK - NAVBODHCHAPTER - गुरुत्वाकर्षण EXERCISE - तथ्यात्मक प्रश्न
18 Videos
- गुरुत्वाकर्षण BOOK - NAVBODHCHAPTER - गुरुत्वाकर्षण EXERCISE - आंकिक उदाहरण
27 Videos
- गतिमान आवेश और चुम्बकत्व BOOK - NAVBODHCHAPTER - गतिमान आवेश और चुम्बकत्व EXERCISE - पाठ्यपुस्तक के प्रशोत्तर
46 Videos
- घर्षण BOOK - NAVBODHCHAPTER - घर्षण EXERCISE - बहुविकल्पीय प्रश्न
30 Videos
Similar Questions
किसी पिंड का भार किसी ग्रह पर किन-किन तथ्यों पर निर्भर करता है?
View Solutionयदि पृथ्वी अपने अक्ष पर घूमना बंद कर दे तो पृथ्वी की सतह पर रखी वस्तु के भार पर क्या प्रभाव पड़ेगा तथा ध्रुव पर रखी वस्तु के भार पर क्या प्रभाव पड़ेगा ?
View Solutionसूर्य से बृहस्पति की दुरी सूर्य से पृथ्वी की दुरी की 5.2 गुनी है। सूर्य के चरों और बृहस्पति का परिभ्र्मण कल ज्ञात कीजिए ।
View Solutionतार की एक वृत्ताकार कुंडली में 100 फेरे हैं, प्रत्येक की त्रिज्या 8.0cm है और इनमे से 0.40A विघुत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुंबकीय क्षेत्र का परिमाण क्या है?
View Solution2 किग्रा द्रव्यमान का संगमरमर का एक गुटका बर्फ पर रखा है | जब इसे 6 मी/से का वेग प्रदान किया जाता है, तो वह 10 सेकण्ड में घर्षण के कारण रुक जाता है | घर्षण गुणांक का मान है -
View SolutionThe lines y=m1x,y=m2xandy=m3x make equal intercepts on the line x+y=1. Then (a) 2(1+m1)(1+m3)=(1+m2)(2+m1+m3) (b)(1+m1)(1+m3)=(1+m2)(1+m1+m3) (c)(1+m1)(1+m2)=(1+m3)(2+m1+m3) (d)2(1+m1)(1+m3)=(1+m2)(1+m1+m3)
View SolutionThe area of the triangle formed by the lines y=m1x+c1,y=m2,x+c2andx=0 is 12(c1+c2)2|m1−m2| b. 12(c1−c2)2|m1+m2| c. 12(c1−c2)2|m1−m2| d. (c1−c2)2|m1−m2|
View SolutionTwo bodies of masses m1andm2 ar placed at a distance r apart. Shows that the position where the gravitational field due to them is zer, the potential is given by
V=−Gr[m1+m2+2√m1m2]
View Solutionसूत्र (m1x2+m2x1m1+m2,m1y2+m2y1m1+m2) क्या कहलाता है ?
View SolutionFαm1m2d2 means F=_____________.
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionIf (m1,1/m1),i=1,2,3,4 are concyclic points, then the value of m1m2m3m4 is
View SolutionIf m1,m2(m1>m2) are the slopes of the lines which make an angle of 30∘ with the line joining the points (1, 2) and (3, 4), then m1m2=
View SolutionConsider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg If m_(1)=10kg, m_(2)=6kg and g =10m//s^(2) then what is the acceleration of masses?
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
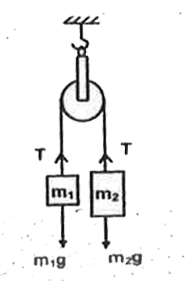
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?
View Solution
