गाउस प्रमेय की सहायता से सिद्ध कीजिए की यदि एक बंद पृष्ठ से गुजरने वाला नेट वैधुत फ्लक्स शून्य है, तो बंद पृष्ठ के अंदर कुल आवेश शून्य है ।

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

मानलो किसी विधुत क्षेत्र →E में एक बेलन (Cy]− inder ) इस प्रकार रखा हुआ है कि उसका अक्ष क्षेत्र →E के समान्तर है ।
बेलन को तीन भागो में विभाजित किया जा सकता है-
(i ) वृत्तीय पृष्ठ S1, (ii ) वृत्तीय पृष्ठ S2 तथा (iii ) वक्र पृष्ठ S3 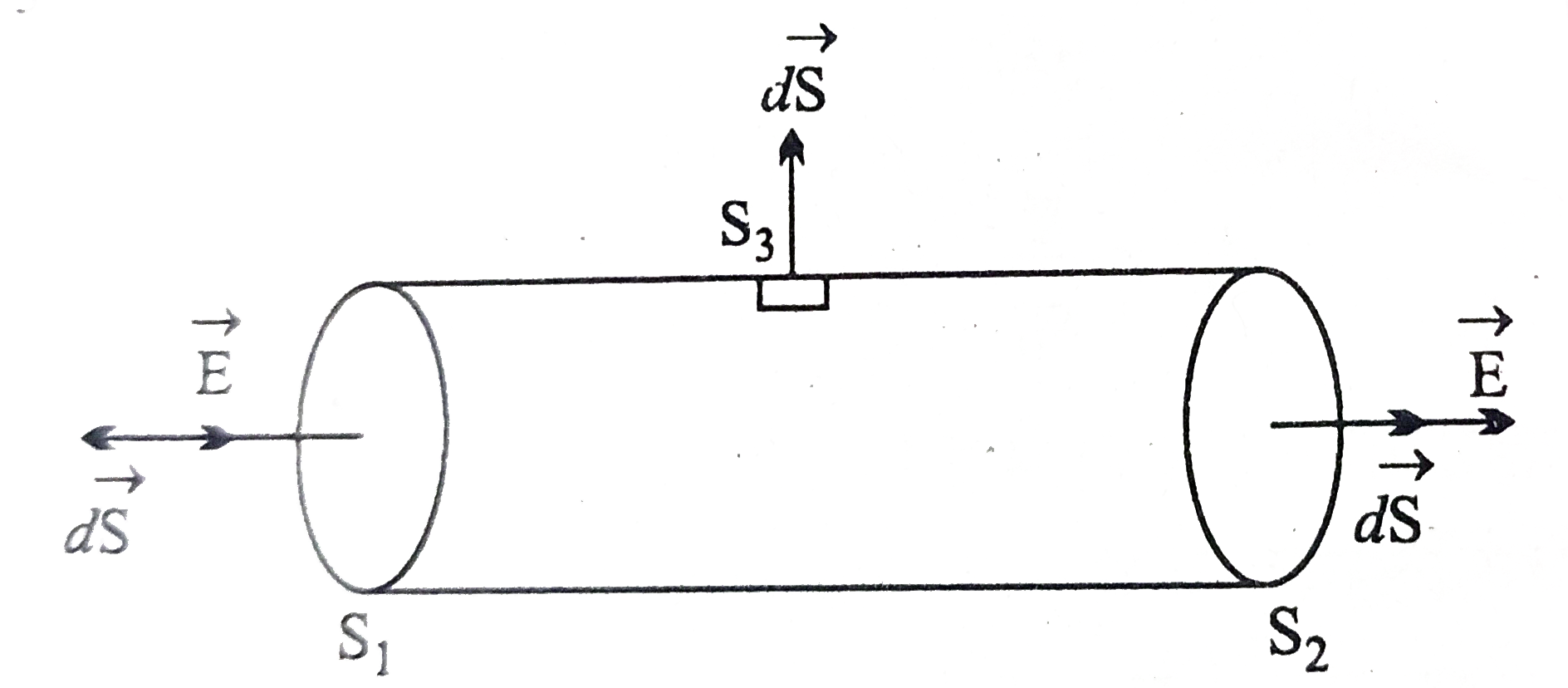ocr_image
वृतीय पृष्ठ S1 से गुजरने वाला विधुत फ्लक्स
ϕ1=∮→E।d→S=∮E।dScos180∘,
[→E और d→S कि दिशाएं विपरीत है । ]
=−E∮dS=−Eπr2,
[∵∮dS=πr2, जहाँ r बेलन कि त्रिज्या है ।]
वृत्तीय पृष्ठ S2 से गुजरने वाला विधुत फ्लक्स
ϕ2=∮→E।→dS=∮E।dScos0∘=E∮dS=Eπr2
वक्र पृष्ठ S3 से गुजरने वाला विधुत फ्लक्स
ϕ3=∮→E।→dS
=∮E।dScos90∘=0, [∵→E⊥d→S]
∴ बेलन से गुजरने वाला नेट वैधुत फ्लक्स
ϕ=ϕ1+ϕ2+ϕ3
=−Eπr2+Eπr2+0=0
बेलन के अंदर कोई आवेश नहीं है ।
अतः यदि एक बंद पृष्ठ से गुजरने वाला नेट वैधुत फ्लक्स शून्य है तो उस बंद पृष्ठ के अंदर कुल आवेश शून्य होता है ।

Updated on:21/07/2023
|
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions