किसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10 cm त्रिज्या के गोलीय गाउसीय प्रस्थ पर वैधुत फ्लक्स −1.0×103Nm2/C∣∣
बिंदु आवेश का मान क्या है ?
दिया है- ϕE=−1.0×103Nm2C−1
q=ϕE.ε0=−1.0×103×8.854×10−12
=−8.854×10−9
=−8.8×10−9C=−8.8nC.
Topper's Solved these Questions
- वैधुत आवेश और क्षेत्र BOOK - NAVBODHCHAPTER - वैधुत आवेश और क्षेत्र EXERCISE - बहुविकल्पीय प्रश्न प्लस
49 Videos
- वैद्युत आवेश तथा क्षेत्रBOOK - NAVBODHCHAPTER - वैद्युत आवेश तथा क्षेत्रEXERCISE - तथ्यात्मक प्रश्न
12 Videos
- संचार व्यवस्था BOOK - NAVBODHCHAPTER - संचार व्यवस्था EXERCISE - NCERT पाठ्य पुस्तक के प्रश्नोत्तर
9 Videos
Similar Questions
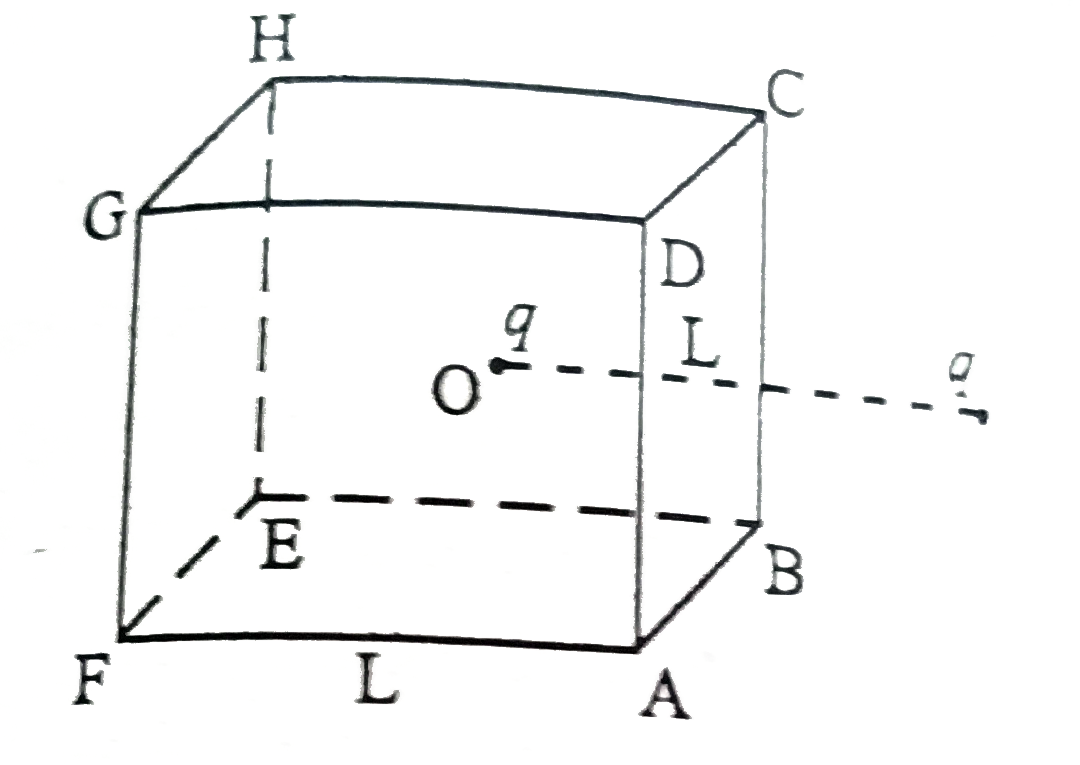
एक आवेश q को L लम्बाई के घन के केंद्र O पर रखा गया है। एकसमान आवेश q केंद्र O से L दुरी पर रखा गया है। फलक ABCD से गुजरने वाला वैधुत फ्लक्स होगा -
View Solutionसामान्य विधूतरोधी होता है , किन्तु वायुयान के रबर टायर कुछ चालक बनाये जाते है , क्यों ?
View Solutionव्योम तरंगो के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित अवृत्तयियो में से कोण -सी आवृतिया उपयुक्त रहेगी -
View Solution2.0μC कोई बिंदु आवेश किसी किनारे पर 9.0 cm किनारे वाले किसी घनीय गॉउसीय पृष्ठ के केंद्र पर स्थिर है ? पृष्ठ से गुजरने वाला नेट फ्लक्स क्या है ?
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionविद्युत क्षेत्र का भौतिक अभिप्राय || बिंदु आवेश के कारण विद्युत् क्षेत्र || आवेशों के निकाय के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionस्थिरवैद्युत विभव | बिंदु आवेश के कारण विभव | आवेशों के निकाय के कारण विभव
View Solutionअतिपरवलय के किसी बिंदु से इसकी अनन्तस्पर्शियों पर डाले गए लंबों का गुणनफल है
View Solutionस्थिरवैद्युत विभव | बिंदु आवेश के कारण विभव | आवेशों के निकाय के कारण विभव
View Solutionबिंदु L बिंदु P(3,4,5) से xz तल पर खींचे गए लंब का पाद बिंदु है | बिंदु L के निर्देशांक है
View Solutionआवेश के विशिष्ट गुण|आवेश एक अदिश राशि है|आवेश सदैव द्रव्यमान के साथ सम्बन्ध होता है|महतवपूर्ण बिंदु|आवेश का स्थानांतरण|आवेश का क्वांटिकरण|आवेश संरक्षित है|OMR|Summary
View Solutionवैद्युत क्षेत्र|बिंदु आवेश के कारण विद्युत क्षेत्र की तीरवता|OMR
View Solutionवैधुत द्विध्रुव प्रश्न|वैधुत द्विध्रुव के कारण किसी भी बिंदु पर वैधुत क्षेत्र|OMR|Summary
View Solutionसमविभव सतह | बिंदु आवेश के कारण विभव | V वी/एस X ग्राफ
View Solutionकिसी वृत्त के जीवा का मध्य बिंदु दिया है
View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
View Solution
