दो समरूप वृत्तीय P और Q जिसमे प्रत्येक कि त्रिज्या R और जिनमे I धारा बह रही है , लम्बवत तलो में इस प्रकार रखे गए है कि उनका केंद्र समतापी है | दोनों तारो ( कुंडलियों ) के समकेन्द्रीय बिन्दु पर कूल चुम्बकीय क्षेत्र ज्ञात कीजिये |
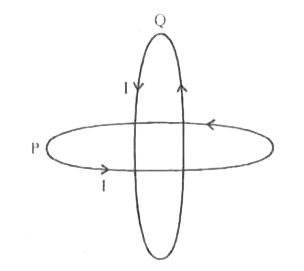
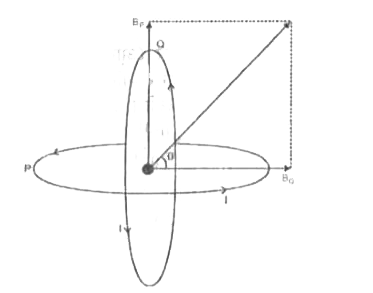
यहाँ ,
ऊर्ध्वाधर दिशा में ऊपर कि ओरहै ओर क्षैतिज दिशा में है | अतः व का परिणामी चुम्बकीय क्षेत्र
एवं ,
अतः नैट चुम्बकीय क्षेत्र दोनों कुंडलियों से पर कार्य कर रहा है |
Topper's Solved these Questions
- विद्युत धारा के चुम्बकीय प्रभाव BOOK - MITTAL PUBLICATIONCHAPTER - विद्युत धारा के चुम्बकीय प्रभाव EXERCISE - पाठ्य निहित उदाहरण
21 Videos
- विद्युत धारा के चुम्बकीय प्रभाव BOOK - MITTAL PUBLICATIONCHAPTER - विद्युत धारा के चुम्बकीय प्रभाव EXERCISE - पाठ्यपुस्तक के प्रश्न एवं उत्तर (बहुचयनात्मक प्रश्न )
13 Videos
- विद्युत धारा के चुम्बकीय प्रभाव BOOK - MITTAL PUBLICATIONCHAPTER - विद्युत धारा के चुम्बकीय प्रभाव EXERCISE - प्रतियोगी परीक्षा संबंधी प्रश्न
26 Videos
- विद्युत चुम्बकीय प्रेरणBOOK - MITTAL PUBLICATIONCHAPTER - विद्युत चुम्बकीय प्रेरणEXERCISE - विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न
14 Videos
- विद्युत धारिता BOOK - MITTAL PUBLICATIONCHAPTER - विद्युत धारिता EXERCISE - प्रतियोगी परीक्षा संबंधी प्रश्न (बहुविकल्पीय प्रश्न )
16 Videos
Similar Questions
एक a भुजा वाले वर्गाकार धारावाही फ्रेम ABCD के केंद्र O पर चुम्बकीय क्षेत्र ज्ञात कीजिये जबकि फ्रेम में I ऐम्पियर माना धारा प्रवाहित हो रही है |
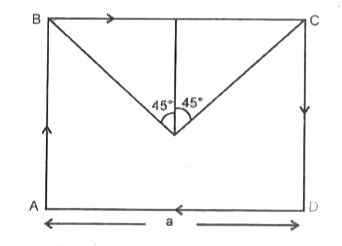
View Solutionकोई आवेशित कण जो एक समान चाल से गति कर रहे है , उत्पन्न करता है |
View Solutionदो एकसमान तार A व B प्रत्येक की लम्बाई l में समान धारा i प्रवाहित है। A को मोड़कर R त्रिज्या का के वृत्त और B को मोड़कर भुजा a का एक वर्ग बनाया जाता है। यदि BA तथा BB क्रमशः वृत्त केंद्र तथा वर्ग के केंद्र पर चुंबकीय क्षेत्र है, तब अनुपात BA/BB होगा :
View Solutionपृथ्वी के चुम्बकीये क्षेत्र 0.30×10−4T के क्षैतिज घटक से समकोण पर पूर्व से पश्चिम तक फैला 20 m लम्बा एक क्षैतिज सीधा तार 5.0ms−1 की चाल से गिर रहा है | तार में प्रेरित विद्युत वाहक बल का तात्क्षणिक मान होगा -
View Solution1.77 μF का एक समान्तर प्लेट संधारित्र एक परावैद्युत (परावैद्युतांक = 200) से निर्मित किया गया है, जिसका क्षयांक भंजक 3×106 वोल्ट/मीटर है। इसी प्रकार के एक संधारित्र जिसका प्लेटों के बीच विभवान्तर 20 वोल्ट है, प्लेटों के बीच की दूरी d तथा क्षेत्रफल A क्रमशः हैं-
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionयदि दो सदिश →a और →b इस प्रकार है कि |→a|=2,∣∣→b∣∣=3 और →a⋅→b=4 तो ∣∣→a−→b∣∣ ज्ञात किजिए।
View Solutionयदि दो घटनाएँ A तथा B इस प्रकार से है कि P(A)=1/4, P(B)=1/2 तथा P(bar A nn bar B) ज्ञात कीजिये।
View Solutionएक दंपत्ति के दो बच्चे है। प्रायिकता ज्ञात कीजिए
दोनों बच्चें लड़कियाँ है , यदि यह ज्ञात है कि बड़ा बच्चा लड़का है।
View Solution
