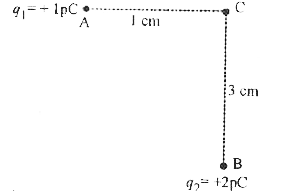
दो बिंदु आवेश +1ρC चित्र के अनुसार क्रमशः बिंदुओं A व B पर रखे है। बिंदु C पर परिणामी विधुत क्षेत्र की तीव्रता ज्ञात कीजिए।
The correct Answer is:92.2NC−1
q1=+1pc=+1×10−12C
q2=+2pC=+2×10−12C
(##MTPDSAHINPHYXIIP1C01E03018_S01.png width=80%><br>बिंदुCपरq_1केकारणउत्पन्नविधुतक्षेत्रकीतीव्रता<br> " " E_ 1 =9xx 10 ^(9) (q_1)/( r_1^(2)) <br> " " = 9xx10 ^(9) (1xx10 ^(-12))/( 0.01xx0.01) <br> " "= 90NC^(-1) (ACकीदिशामें)<br>इसीप्रकारCबिंदुपर+q_2केकारणउत्पन्नविधुतक्षेत्रकीतीव्रता<br> " "E_2 =9xx10 ^(9) (q_2)/( r_2^(2))<br> " " = 9xx10 ^(9) (2xx10 ^(-12) )/( 0.03xx0.03) <br> " " = 20NC^(-1) (BCदिशामें)<br> because angle ACB = 90^(@) अतः oversetto (E_1) व oversetto (E_2) परस्परलंबवतहोंगें।<br> therefore Cपरपरिणामीविधुतक्षेत्रकीतीव्रता<br> " " oversetto E=oversetto (E_1)+ oversetto (E_2) <br> " " E=sqrt(E_1^(2) + E_2^(2))<br>" "= sqrt( ( 90 )^(2) +(20 ) ^(2))<br> " "= sqrt( 8100+400) <br>" "= sqrt( 8500) = 10 sqrt( 85) = 10 xx9.22<br> " " E= 92.2NC^(-1)
Topper's Solved these Questions
- विधुत क्षेत्र BOOK - MITTAL PUBLICATIONCHAPTER - विधुत क्षेत्र EXERCISE - प्रतियोगी परीक्षा सम्बन्धी प्रश्न
17 Videos
- विधुत क्षेत्र BOOK - MITTAL PUBLICATIONCHAPTER - विधुत क्षेत्र EXERCISE - अन्य महत्वपूर्ण प्रश्न (दीर्घ उत्तरीय प्रश्न )
9 Videos
- विद्युत विभव BOOK - MITTAL PUBLICATIONCHAPTER - विद्युत विभव EXERCISE - प्रतियोगी परीक्षा संबंधी प्रश्न
15 Videos
Similar Questions
एक आवेश Q वर्ग के प्रत्येक विपरीत कोने पर रखा है। एक आवेश q प्रत्येक अन्य दो कोनों पर रखा है। यदि Q पर नेट विधुत क्षेत्र शून्य बल हो तो Qq बराबर होगा।
View Solutionप्रेरण द्वारा आवेश की व्याख्या कीजिए।
View Solutionनिम्न में कौन-सा/से कथन सत्य है/हैं ?
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionदो स्थिर बिंदु A और B के निर्देशांक क्रमशः (a,0) और (−a,0) है , तो चर बिंदु P का बिन्दुपथ ज्ञात कीजिए जबकि :
PA=nPB , जहाँ n अचर है ।
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View SolutionA और B दो बिंदु है। बिंदुओं A और B के स्थिति क्रमशः 6¯a−2¯b और ¯b−9¯a है। वह अनुपात ज्ञात कीजिए जिसमें बिंदु P जिसका स्थिति सदिश ¯a−¯b है रेखाखण्ड AB को विभाजित करता है।
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solutionवलय के अक्ष पर स्थित बिंदु पर विधुत क्षेत्र की तीव्रता
View Solutionवैद्युत क्षेत्र|बिंदु आवेश के कारण विद्युत क्षेत्र की तीरवता|OMR
View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
View Solutionवैधुत बल व गुर्त्वाकर्षण बल में अंतर #!#निलंबन बिंदु आवेश व कुलाम्ब के नियम पर आधारित महत्वपूर्ण प्रशन
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solutionसमान रूप से आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता व उस पर आधारित प्रशन
View Solution
