द्रव्यमान M तथा त्रिज्या R का एक छल्ला अपने केंद्र से होकर जाने वाली स्थिर ऊर्ध्वाधर अक्ष के परितः कोणीय वेग ω से घूम रहा है। इस क्षण M/8 द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केंद्र O पर विराम स्थिति में है। वो दर्शाये चित्रानुसार छल्ले पर लगी द्रव्यमानहीन दो छड़ों पर त्रिज्यतः बाहर की ओर गति कर सकतेक हैं किसी क्षण पर निकाय की कोणीय गति 89ω है तथा बिंदु द्रव्यमान O से 35R दूरी पर है। इस क्षण दूसरे बिंदु द्रव्यमान की O से दूरी होगी:
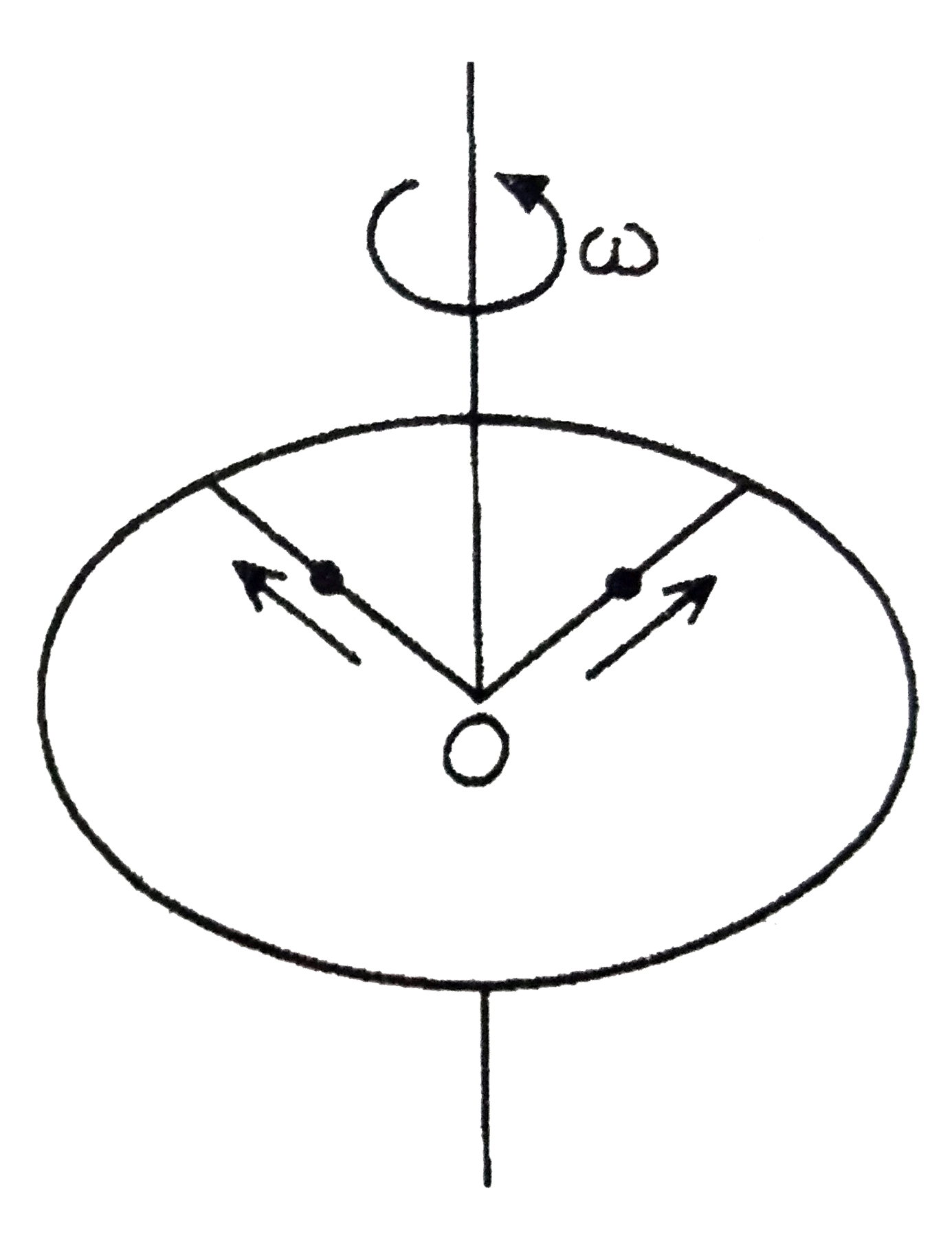
23R
13R
35R
45R
The correct Answer is:D
माना इस क्षण अन्य द्रव्यमान केंद्र O से x दूरी पर है। कोणीय संवेग संरक्षण के नियम से
I1ω1=I2ω2
∴(MR2)(ω)=[MR2+M8(35R)2+M8x2](89ω)
हल करने पर x=45R
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - बहुविकल्पीय प्रश्न II11videos
घूर्णन गति
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - सत्य/असत्य3videos
घूर्णन गति
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गुरुत्वाकर्षण EXERCISE - विश्लेषणात्मक प्रश्न5videos
गुरुत्वाकर्षण
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद iii )2videos
चुम्बकत्व
Similar Questions
लम्बाई 6a तथा द्रव्यमान 8m की एकसमान छड़, चिकनी क्षैतिज मेज पर रखी है। m तथा 2m द्रव्यमान के दो बिंदु द्रव्यमान क्रमशः 2v तथा v वेग से गति करते हुए चित्रानुसार दण्ड से टकराते हैं तथा चक्कर के बाद छड़ से चिपक जाते हैं। यदि द्रव्यमान केंद्र के परितः कोणीय वेग, द्रव्यमान केंद्र का वेग तथा कुल ऊर्जा E क्रमशः ω,vC तथा E हो तो टक्कर के उपरांत
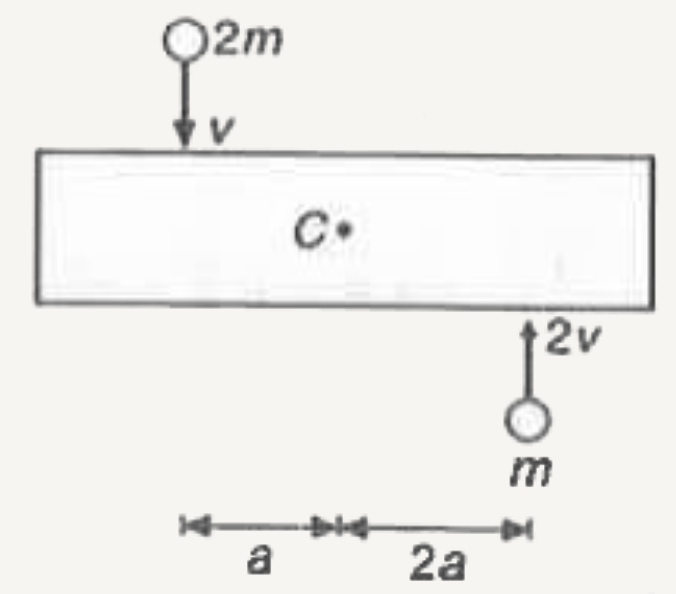 04:32View Solution
04:32View Solutionएकसमान मोटाई व घनत्व की एक त्रिभुजाकार प्लेट कागज के तल के लम्बवत अक्ष के परितः घुमायी जाती है। यह प्लेट AB के मध्य बिंदु C पर कार्य करने वाले बल F द्वारा जिस अक्ष के परितः घुमायी जाती है वह (a) A बिंदु से (b) B बिंदु से जाती है। दोनों स्थितियों a व b में कोणीय त्वरण समान होगा।
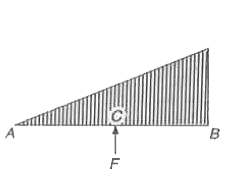 02:29View Solution
02:29View Solutionदो उपग्रह S1 व S2 एक ग्रह के चारों ओर समतलीय वृत्ताकार कक्षाओं में एक ही दिशा में घूमते हैं। उनके परिक्रमण काल क्रमश: 1 घण्टा व 8 घण्टा हैं। S1 की कक्षा की त्रिज्या 104 किमी है। जब S2,S1 के निकटस्थ है तो ज्ञात कीजिए (a) S1 के सापेक्ष S2 की चाल, (b) S1 में बैठे अन्तरिक्ष यात्री द्वारा वास्तविक रूप से प्रेक्षित S2 की कोणीय चाल।
50:04View Solutionदर्शाए चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा । धनात्मक दिशा में प्रवाहित हो रही है। पट्टी की लम्बाई, चौड़ाई तथा मोटाई क्रमश: 1, wतथा d हैं। पट्टी पर धनात्मक दिशा में एकसमान चुम्बकीय क्षेत्र B लगाया गया हैं। जिसके कारण आवेशवाहक :-दिशा की ओर विक्षेपित होते हैं। परिणामतः सतह PORS पर आवेशवाहकों का संचयन होता है तथा PORS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है। तब एक विभवान्तर --दिशा के साथ विकसित होता है। आवेशवाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से सन्तुलित नहीं हो जाता। विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है
Q एक ही चालक पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) लें। उनकी लम्बाइयाँ बराबर हैं, चौडाइयाँ क्रमश:w1 एवं w2 तथा मोटाइयाँ क्रमश: d1 तथा d2 हैं। दो बिन्दु K तथा Mx-y तल के समान्तर आमने-सामने के फलकों पर स्थित हैं। पट्टियों । तथा 2 में K तथा M के बीच विभवान्तर क्रमश: V1 तथा V2 हैं। तब उनमें बहने वाली एक दी गई विद्युत धारा / तथा एक दी गई चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)56:20View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
01:01:25View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
38:22View Solutionद्रव्यमान केंद्र की गति व कणो के निकाय का रेखीय संवेग
01:25:34View Solutionविभिन्न वस्तुओं का द्रव्यमान केंद्र।द्रव्यमान केंद्र की गति व कणो के निकाय का रेखीय संवेग
01:22:42View Solutionकोणीय संवेग संरक्षण का नियम | गुरुत्व केंद्र | गुरुत्व केंद्र तथा द्रव्यमान केंद्र में अंतर | कुछ प्रश्न
01:30:34View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
01:21:36View Solutionद्रव्यमान केंद्र पर महत्वपूर्ण उधारण
01:12:55View Solutionखंडित वस्तुओं का द्रव्यमान केंद्र |द्रव्यमान केंद्र की गति
43:31View Solutionद्रव्यमान केंद्र की गति
38:02View Solutionद्रव्यमान केंद्र की गति
29:57View Solutionद्रव्यमान केंद्र की गति#!#द्रव्यमान केंद्र ज्ञात करना
55:56View Solutionदो द्रव्यमान या दो से अधिक द्रव्यमान के मध्य सापेक्षिक गति
01:21:28View Solution

