चित्र में दिखाये निकाय के हिस्से हैं : (i) 3R बाहरी–त्रिज्या की वलय, जो क्षैतिज सतह पर ω कोणीय चाल से दक्षिणावर्त बिना फिसले लुढ़क रही है, और (ii) 2R त्रिज्या की भीतरी चकती जो ω/2 कोणीय चाल से वामावर्त घूम रही है। घर्षण-रहित बॉल-बियरिंग (गोलियाँ) वलय और डिस्क को एक दूसरे से अलग रखते हैं। निकाय x-z तल में है। भीतरी डिस्क पर बिंदु P मूल बिन्दु से R दूरी पर है और OP क्षैतिज से 30∘ का कोण बनाता है। तब क्षैतिज सतह के सापेक्ष
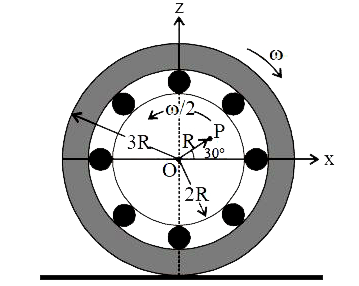
बिंदु O का रेखीय वेग 3Rωˆi
बिंदु P का रेखीय वेग 114Rωˆi+√34Rωˆk है
बिंदु P का रेखीय वेग 134Rωˆi−√34Rωˆk है
बिंदु P का रेखीय वेग (3−√34)Rωˆi+14Rωˆk है
The correct Answer is:A, C
बिंदु O पर संवेग
vO=(3Rω)

PO=−Rω2sin30∘+Rω2cos30∘
=−Rω4+√3Rω4
परंतु PO=P−O
∴P=PO+O
=(−Rω4+√3Rω4)+3Rω
=114Rω+√34Rω
Topper's Solved these Questions
- घूर्णन गतिBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - सत्य/असत्य
3 Videos
- घूर्णन गतिBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - रिक्त स्थानों की पूर्ति कीजिए
7 Videos
- घूर्णन गतिBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - श्रृंखलाबद्ध बोधन प्रकार
10 Videos
- गुरुत्वाकर्षण BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गुरुत्वाकर्षण EXERCISE - विश्लेषणात्मक प्रश्न
5 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद iii )
2 Videos
Similar Questions
एकसमान मोटाई व घनत्व की एक त्रिभुजाकार प्लेट कागज के तल के लम्बवत अक्ष के परितः घुमायी जाती है। यह प्लेट AB के मध्य बिंदु C पर कार्य करने वाले बल F द्वारा जिस अक्ष के परितः घुमायी जाती है वह (a) A बिंदु से (b) B बिंदु से जाती है। दोनों स्थितियों a व b में कोणीय त्वरण समान होगा।
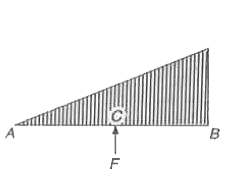
View Solutionएक समरूप घन जिसकी भुजा a तथा द्रव्यमान m है एक रूक्ष क्षैतिज मेज पर रखा है । इस घन के किसी एक फलक के लम्बवत क्षैतिज बल F, फलक के केंद्र के ठीस ऊपर आधार से 3a/4 की ऊंचाई पर लगाया जाता है। बल F का न्यूनतम मान............ होने पर घन की एक कोर के परितः उठना प्रारंभ हो जाएगा। मान लीजिए कि घन फिसलता नहीं है।
View Solutionदो डिस्कें A तथा B एक ऊर्ध्वाधर धुरी पर समाक्ष रूप से अवस्थिरत की गई है। उभयनिष्ठ अक्ष के परितः उन चकतियों के जड़त्व आघूर्ण क्रमशः I तथा 2I है। एक स्पि्रंग को x1 दूरी से दबाकर उसकी सम्पूर्ण स्थितिज ऊर्जा का उपयोग करके, चकती A को प्रारंभिक कोणीय वेग 2ω दिया जाता है। उतने ही स्पि्रंग गुणांक वाले एक दूसरे स्पि्रंग को x2 दूरी से दबाकर डिस्क B को कोणीय वेग ω दिया जाता है। दोनों चकतियां दक्षिणावर्त दिशा में घूम रही हैं
अनुपात x1/x2 है।
View Solutionदो उपग्रह S1 व S2 एक ग्रह के चारों ओर समतलीय वृत्ताकार कक्षाओं में एक ही दिशा में घूमते हैं। उनके परिक्रमण काल क्रमश: 1 घण्टा व 8 घण्टा हैं। S1 की कक्षा की त्रिज्या 104 किमी है। जब S2,S1 के निकटस्थ है तो ज्ञात कीजिए (a) S1 के सापेक्ष S2 की चाल, (b) S1 में बैठे अन्तरिक्ष यात्री द्वारा वास्तविक रूप से प्रेक्षित S2 की कोणीय चाल।
View Solutionदर्शाए चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा । धनात्मक दिशा में प्रवाहित हो रही है। पट्टी की लम्बाई, चौड़ाई तथा मोटाई क्रमश: 1, wतथा d हैं। पट्टी पर धनात्मक दिशा में एकसमान चुम्बकीय क्षेत्र B लगाया गया हैं। जिसके कारण आवेशवाहक :-दिशा की ओर विक्षेपित होते हैं। परिणामतः सतह PORS पर आवेशवाहकों का संचयन होता है तथा PORS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है। तब एक विभवान्तर --दिशा के साथ विकसित होता है। आवेशवाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से सन्तुलित नहीं हो जाता। विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है
Q एक ही चालक पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) लें। उनकी लम्बाइयाँ बराबर हैं, चौडाइयाँ क्रमश:w1 एवं w2 तथा मोटाइयाँ क्रमश: d1 तथा d2 हैं। दो बिन्दु K तथा Mx-y तल के समान्तर आमने-सामने के फलकों पर स्थित हैं। पट्टियों । तथा 2 में K तथा M के बीच विभवान्तर क्रमश: V1 तथा V2 हैं। तब उनमें बहने वाली एक दी गई विद्युत धारा / तथा एक दी गई चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionवक्र y=xex2 की वह स्पर्श रेख जो बिंदु (1,e) से होकर जाती है, निम्न में से किस बिंदु से भी होकर जाती है ?
View Solutionवक्र y=x2−5x+5 की स्पर्श रेखा, जो रेखा 2y=4x+1 के समांतर है, निम्न में से किस बिन्दु से होकर जाती है
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionनिम्नलिखित कॉलम को सुमेलित कीजिये
कॉलम-I कॉलम-II(A) एक समान आवेशित परावैधुत वलय(p) निकाय के बाहर नियत स्थिर विधुत क्षेत्र है(B) एक सामान आवेशित परावैधुत वलय कोणीय वेग ωसे घूर्णित है (q)चुम्बकीय क्षेत्र की तीव्रता(C) वलय में नियत धारा i(r)वैधुत क्षेत्र (प्रेरित)(D)i=i0cosωt(s) चुम्बकीय द्वि - ध्रुव आघूर्ण
View Solutionउस वृत्त का समीकरण जिसका केन्द्र x-अक्ष पर है तथा त्रिज्या 4 है। और जो मूल बिन्दु से होकर जाता है, होगा
View SolutionEquation of the circle whose center x-अक्ष पर है तथा त्रिज्या 4 है। और जो मूल बिन्दु से होकर जाता है, होगा
View Solutionजो चीजों से उठती अंधेपन की भाप पर दुलक जाती है' में कौन-सा अलंकार है ?
View Solutionअलग-अलग जगहों पर खड़िया-पट्टी के अलग-अलग नामों में से एक है
View Solution
