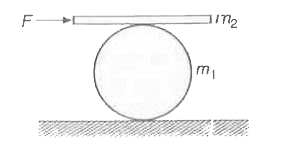
एक व्यक्‍ति $m_{1}$ द्रव्यमान के बेलन को $m_{2}$ द्रव्यमान के तख्ते से धकेलता है किसी भी संपर्क पर फिसलन नहीं है। व्यक्‍ति द्वारा आरोपित बल का क्षैतिज घटक F है। ज्ञात कीजिए-
(a) तख्ते तथा बेलन के द्रव्यमान केंद्रों के त्वरण तथा
(b) सम्पर्क बिंदुओं पर घर्षण बलों के परिमाण व दिशाएं।

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(a) $a_{C M} = \frac{4 F}{3 m_{1} + 8 m_{2}}, a_{तख्‍ता} = \frac{8 F}{3 m_{1} + 8 m_{2}} = 2 a_{C M}$
(b) $\frac{3 F m_{1}}{3 m_{1} + 8 m_{2}}, \frac{F m_{1}}{3 m_{1} + 8 m_{2}}$

विभिन्न सम्पर्क बिंदुओं पर हम घर्षण बल की स्वेच्छ दिशाएं चुन सकते हैं। अन्‍तिम परिणाम में ऋणातमक मान विपरीत दिशाएं प्रदर्शित करेंगे।

माना तख्ते तथा बेलन के बीच घर्षण बल $f_{2}$ तख्ते का त्वरण $a_{2}$ तथा बेलन का उसके द्रव्यमान केंद्र के परितः कोणीय त्वरण $α$ है।
चूंकि कहीं भी फिसलन नहीं है अतः

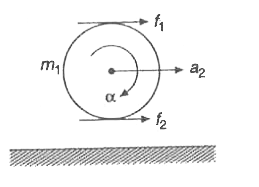
$a_{1} = 2 a_{2}$ ……(i)
$a_{1} = \frac{F - f_{1}}{m_{2}}$ ………ii
$a_{2} = \frac{f_{1} + f_{2}}{m_{1}}$ …………iii
$α = \frac{(f_{1} - f_{2}) R}{I} = \frac{(f_{1} - f_{2}) R}{\frac{1}{2} m_{1} R^{2}}$
या $α = \frac{2 (f_{1} - f_{2})}{m_{1} R^{2}}$
$a_{2} = α R = \frac{2 (f_{1} - f_{2})}{m_{1}}$
(a) उपरोक्त समीकरणों को हल करने पर
$a_{1} = \frac{8 F}{3 m_{1} + 8 m_{2}}$
तथा $a_{2} = \frac{4 F}{3 m_{1} + 8 m_{2}}$
(b) घर्षणबल $f_{1} = \frac{3 m_{1} F}{3 m_{1} + 8 m_{2}}, f_{2} = \frac{m_{1} F}{3 m_{1} + 8 m_{2}}$
चूंकि सभी राशियां धनात्मक है इसलिए चित्र में सही रूप से दर्शाई गईं है।

|

Updated on:21/07/2023

Class 12 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

JEE Main & Advanced (Hindi Medium)-घूर्णन गति-विश्लेषणात्मक प्रश्न

Home
Ask Doubt
Profile