निम्न समीकरणें अनुप्रस्थ तरंगे दर्शाती है
z1=Acos(kx−ωt),z2=Acos(kx+ωt),z3=Acos(ky−ωt)
तरंगो के कौन - से संयोजन
(a) अप्रगामी तरंग,
(b) , धन x तथा धन y - अक्षो से 45∘ का कौन बनाते हुए चलने वाली तरंग प्रदर्शित करते है ? प्रत्येक दशा में वे स्थितियाँ ज्ञात कीजिए जहाँ पर परिणामी तीव्रता सदैव शून्य रहती है ?
The correct Answer is:(a) z1 तथा z2;x=(2n+1)π2k जहाँ n=0,±1±2 . . .
(b) z1 तथा z3x−y=(2n+1)πk जहाँ n=0,±1±2 . . .
(a) एक अप्रगामी तरंग बनाने वाली दो तरंगे समरूप होनी चाहिए तथा एक दूसरे की विपरीत दिशा में गतिमान होनी चाहिए।
अतः z1 तथा z2 एक अप्रगामी तरंगे निर्मित करेगी।
इस स्थिति में अप्रगामी तरंग की समीकरण
z=z1+z2=Acoskxcosωt=Axcosωt जहाँ Ax=2Acoskx
उन स्थानों पर जहाँ Ax=0 है , परिणामी तीव्रता शून्य होगी।
Ax=0 का अर्थ है कि
kx=(2n+1)π2 जहाँ n=0,±1,±,2,....
या x=(2x+1)π2kजहाँ n=0,±,1,±,2,....
(b) z1 धन x- अक्ष में गतिमान तरंग है जबकि z3 धन y- अक्ष में गतिमान तरंग है।
z1 व z3 के अध्यारोपण के फ़लस्वरुप ऐसी तंरग निर्मित होगी जो धन x-अक्ष धन y- धन अक्ष में गतिमान होगी , इस तरंग का समीकरण
z=z1+z3=2Acos[kx+ky2−ωt]cos(kx−ky2)
परिणामी तीव्रता शून्य है , जहाँ cosk(x−y2)=0
या k(x−y)2=(2n+1)π2
या (x−y)=(2n+1)πk जहाँ n=0,±,1,±,2,....
Topper's Solved these Questions
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद I )
3 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद II )
3 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - एकल पूर्णांक उत्तर प्रकार
4 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद iii )
2 Videos
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
Similar Questions
दो समतल गुनावृत्ति ध्वनि तरंगे (Plane harmonic sound waves) निम्न समीकरणों से प्रदर्शित की जाती है :
y1(x,t)=Acos(0.5πx−100πt)
y2(x,t)=Acos(0,46πx−92πt)
(सभी प्राचल एम. के. एस. पध्दति में है )
एक प्रेक्षक एक सेकण्ड में कितनी बार अधिकतम तीव्रता सुनता है ?
View SolutionPassage-II
दो रेलगाड़ियाँ A तथा B क्रमशः 20m/s तथा 30m/s की चाल से समान दिशा तथा पथ पर गतिमान है। B, A आगे है। इंजिन प्रारम्भिक सिरों पर है। A का इंजिन एक लम्बी सीटी बजता है। सीटी की ध्वनि को आवृति में परिवर्तन f1=800Hz से f2=1200Hz तक के घटको में युक्त मन जाये (चित्रानुसार)। इस प्रकार आवृत्ति में फैलाव (आवृत्ति-निम्नतम आवृत्ति), 320Hz है। ध्वनि का वेग 340m/sरहता है।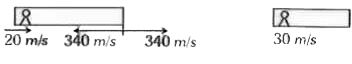
सीटी की ध्वनि की चाल है
View Solution1.0 ग्राम द्रव्यमान की 20 सेमी लम्बी डोरी के दोनों सिरे स्थिर रखें गये है तथा इस रस्सी में 0 . 5 न्यूटन का तनाव है। 100 हर्ट्ज के किसी बाह्य कम्पित (Vibrator) के द्वारा इस डोरी में कम्पन पैदा किये जाते है , कम्पित डोरी के दो उत्तरोत्तर निस्पन्दो (Successive nodes) के बीच की दुरी (सेमी में) निकालें।
View Solutionदर्शाए चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा । धनात्मक दिशा में प्रवाहित हो रही है। पट्टी की लम्बाई, चौड़ाई तथा मोटाई क्रमश: 1, wतथा d हैं। पट्टी पर धनात्मक दिशा में एकसमान चुम्बकीय क्षेत्र B लगाया गया हैं। जिसके कारण आवेशवाहक :-दिशा की ओर विक्षेपित होते हैं। परिणामतः सतह PORS पर आवेशवाहकों का संचयन होता है तथा PORS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है। तब एक विभवान्तर --दिशा के साथ विकसित होता है। आवेशवाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से सन्तुलित नहीं हो जाता। विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है
Q एक ही चालक पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) लें। उनकी लम्बाइयाँ बराबर हैं, चौडाइयाँ क्रमश:w1 एवं w2 तथा मोटाइयाँ क्रमश: d1 तथा d2 हैं। दो बिन्दु K तथा Mx-y तल के समान्तर आमने-सामने के फलकों पर स्थित हैं। पट्टियों । तथा 2 में K तथा M के बीच विभवान्तर क्रमश: V1 तथा V2 हैं। तब उनमें बहने वाली एक दी गई विद्युत धारा / तथा एक दी गई चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)
View Solutionहर प्रकार की गतिकीय समस्याओं के निश्लेषण के लिए कला-समष्टि चित्रा (Phase space diagrams) का उपयोग किया जाता है। प्रारम्भिक दशा, स्थिति व संवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझने में बहुत उपयोगी है। यहाँ हम एकविमीय सरल गतिकीय निकायों की बात करते हैं। इनके लिए कला-समष्टि समतल है जिसमें स्थिति X-अक्ष पर तथा संबेग Y-अक्ष पर रखते हैं, तब कुला-समष्टि चित्र इस समतल में एक x(t)-p(t) वक्र होगा। वक्र पर तीर समय बढ़ने की दिशा को दर्शाता है।
उदाहरण के लिए, स्थिर वेग से चल रहे कण के लिए कला- समष्टि चित्रा है, सरल रेखा है, जिसे चित्र में दिखाया गया है। चिह्न परिपाटी में स्थिति या संवेग को ऊपर (या दाहिने) ओर धनात्मक तथा नीचे (या बाई) ओर ऋणात्मक माना जाता है।
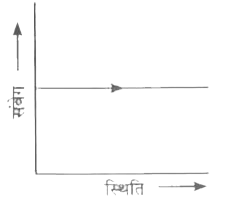
1. जमीन से ऊपर की ओर फेंकी गई गेंद का कला-समष्टि चित्रा है।
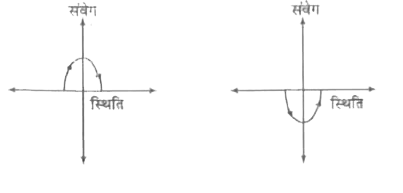
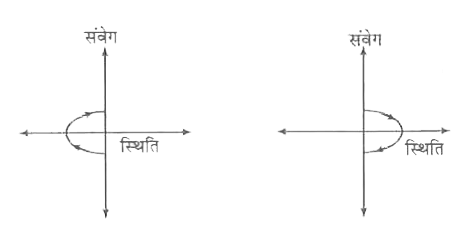
View SolutionThe following equations represent progressive transverse waves
z1=Acos(ωt−kx)
z2=Acos(ωt+kx)
z3=Acos(ωt+ky)
z4=Acos(2ωt−2ky)
A stationary wave will be formed by superposing
View SolutionFollowing are equations of four waves : (i) y_(1) = a sin omega ( t - (x)/(v)) (ii) y_(2) = a cos omega ( t + (x)/(v)) (iii) z_(1) = a sin omega ( t - (x)/(v)) (iv) z_(1) = a cos omega ( t + (x)/(v)) Which of the following statements are correct ?
View SolutionConsider the three waves z1,z2andz3 as
z1=Asin(kx−ωt)
z2=Asin(kx+ωt)
z3=Asin(ky−ωt)
Which of the following represents a standing wave?
View SolutionWhich two of the given transverse waves will give stationary waves when get superimposed z_(1) =a cos (kx- omega t) " " .....(A) z_(2) =a cos (kx+ omega t) " " .....(B) z_(3) =a cos (kx- omega t) " " .....(C)
View SolutionWhich two of the given transverse waves will give stationary wave when get superimposed? z_(1) = a cos (kx-omegat) " "(A) z_(2) = a cos (kx +omegat) " "(B) z_(3) = a cos (ky - omegat) " "(C )
View Solutiony_(1) = 4 sin (omega t + kx), y_(2) =-4 cos(omega t + kx) , the phase difference is
View SolutionThree transverse progressive waves are z_(1) = A cos (kx - omega t) , z_(2) = A cos (ks + omega t) and z_(3) = A cos (ky - omega t) . How may these be superposed to generate (i) a stationary wave, (ii) a wave propagating in a direction inclined at an angle of 45^(@) with both the positive x and y - axes ? In each case, find out the positions where the resultant intensity would always be zero .
View SolutionFollowing are equations of four waves (i) y _(1) a sin omega (t - (x)/(v)) (ii) y_(2) = a cos omega (t + (x)/(v)) (iii) z_(1) = a sin omega (t - (x)/(v)) (iv) z_(2) = a cos omega (t + (x)/(v)) Which of the following statements are correct ?
View Solutionx=cos(ωt+kx) संबंध में ω का विमा होगा
View SolutionThree transverse waves are represented by
y1=Acos(kx−ωt)
y2=Acos(kx+ωt)
y3=Acos(ky−ωt)
The combination of waves which can produce stationary waves is
View Solution
