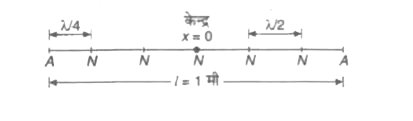
1 मी लम्बी धातु की छड़ को उसके मध्य - बिन्दु पर दृढ़तापूर्वक कसा गया है छड़ में अनुदैर्ध्य अप्रगामी तरंग इस प्रकार उत्पन्न की गई है कि मध्य बिन्दु दोनों ओर दो - दो निस्पन्द बनते है। एक प्रस्पंन्द का आयाम 2×10−6 मी है। मध्य बिन्दु से 2 सेमी दूर बिन्दु पर गति की समीकरण तथा छड़ में अवयव तरंगो की समीकरणें ज्ञात कीजिए (यंग गुणांक Y=2×1011 न्यूटन / मी2, घनत्व किग्रा / मी3 )
The correct Answer is:y=2×10−6sin(0.1π)sin(25000πt)
छड़ में अनुदैर्ध्य तरंगो की चाल v=√Yρ=√2×10118000=5000 मी / से
प्रस्पन्द पर आयाम = 2A ( यहाँ A, अवयव तरंगो का आयाम है)
=2×10−6 मी
∴A=10−6 मी
अब l=5λ2
⇒λ=2l5=2(1.0)5=0.4 मी
अतः मध्य बिन्दु से x दुरी पर गति की समीकरण है
y=2Asinkxsinωt
यहाँ k=2π0.4=5π
ω=2πf=2πvλ=2π(50000.4)=25000π रेडिएन / से
∴y=(2×10−6)sin(5πx)sin(25000πt)
x=2×10−2 मी पर
y=(2×10−6)sin(5π×2×10−2sin(25000πt)
=(2×10−6)sin(0.1π)sin(25000πt)
(b) अवयव तरंगो की समीकरणे है
y1=Asin(ωt−kx) तथा y2=Asin(ωt+kx)
या y1=10−6sin(25000πt−5πt)
तथा y2=10−6sin(25000πt+5πx)
Topper's Solved these Questions
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद I )
3 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - श्रंखलाबद्ध - बोधन प्रकार (अनुच्छेद II )
3 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - एकल पूर्णांक उत्तर प्रकार
4 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद iii )
2 Videos
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
Similar Questions
दो समतल गुनावृत्ति ध्वनि तरंगे (Plane harmonic sound waves) निम्न समीकरणों से प्रदर्शित की जाती है :
y1(x,t)=Acos(0.5πx−100πt)
y2(x,t)=Acos(0,46πx−92πt)
(सभी प्राचल एम. के. एस. पध्दति में है )
एक प्रेक्षक एक सेकण्ड में कितनी बार अधिकतम तीव्रता सुनता है ?
View SolutionPassage-II
दो रेलगाड़ियाँ A तथा B क्रमशः 20m/s तथा 30m/s की चाल से समान दिशा तथा पथ पर गतिमान है। B, A आगे है। इंजिन प्रारम्भिक सिरों पर है। A का इंजिन एक लम्बी सीटी बजता है। सीटी की ध्वनि को आवृति में परिवर्तन f1=800Hz से f2=1200Hz तक के घटको में युक्त मन जाये (चित्रानुसार)। इस प्रकार आवृत्ति में फैलाव (आवृत्ति-निम्नतम आवृत्ति), 320Hz है। ध्वनि का वेग 340m/sरहता है।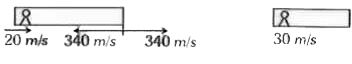
सीटी की ध्वनि की चाल है
View Solution1.0 ग्राम द्रव्यमान की 20 सेमी लम्बी डोरी के दोनों सिरे स्थिर रखें गये है तथा इस रस्सी में 0 . 5 न्यूटन का तनाव है। 100 हर्ट्ज के किसी बाह्य कम्पित (Vibrator) के द्वारा इस डोरी में कम्पन पैदा किये जाते है , कम्पित डोरी के दो उत्तरोत्तर निस्पन्दो (Successive nodes) के बीच की दुरी (सेमी में) निकालें।
View Solutionदर्शाए चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा । धनात्मक दिशा में प्रवाहित हो रही है। पट्टी की लम्बाई, चौड़ाई तथा मोटाई क्रमश: 1, wतथा d हैं। पट्टी पर धनात्मक दिशा में एकसमान चुम्बकीय क्षेत्र B लगाया गया हैं। जिसके कारण आवेशवाहक :-दिशा की ओर विक्षेपित होते हैं। परिणामतः सतह PORS पर आवेशवाहकों का संचयन होता है तथा PORS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है। तब एक विभवान्तर --दिशा के साथ विकसित होता है। आवेशवाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से सन्तुलित नहीं हो जाता। विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है
Q एक ही चालक पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) लें। उनकी लम्बाइयाँ बराबर हैं, चौडाइयाँ क्रमश:w1 एवं w2 तथा मोटाइयाँ क्रमश: d1 तथा d2 हैं। दो बिन्दु K तथा Mx-y तल के समान्तर आमने-सामने के फलकों पर स्थित हैं। पट्टियों । तथा 2 में K तथा M के बीच विभवान्तर क्रमश: V1 तथा V2 हैं। तब उनमें बहने वाली एक दी गई विद्युत धारा / तथा एक दी गई चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)
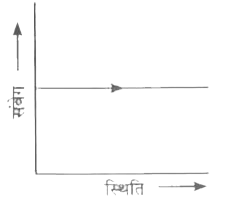
View Solutionहर प्रकार की गतिकीय समस्याओं के निश्लेषण के लिए कला-समष्टि चित्रा (Phase space diagrams) का उपयोग किया जाता है। प्रारम्भिक दशा, स्थिति व संवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझने में बहुत उपयोगी है। यहाँ हम एकविमीय सरल गतिकीय निकायों की बात करते हैं। इनके लिए कला-समष्टि समतल है जिसमें स्थिति X-अक्ष पर तथा संबेग Y-अक्ष पर रखते हैं, तब कुला-समष्टि चित्र इस समतल में एक x(t)-p(t) वक्र होगा। वक्र पर तीर समय बढ़ने की दिशा को दर्शाता है।
उदाहरण के लिए, स्थिर वेग से चल रहे कण के लिए कला- समष्टि चित्रा है, सरल रेखा है, जिसे चित्र में दिखाया गया है। चिह्न परिपाटी में स्थिति या संवेग को ऊपर (या दाहिने) ओर धनात्मक तथा नीचे (या बाई) ओर ऋणात्मक माना जाता है।
1. जमीन से ऊपर की ओर फेंकी गई गेंद का कला-समष्टि चित्रा है।
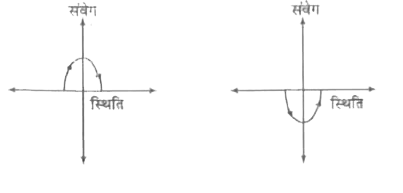
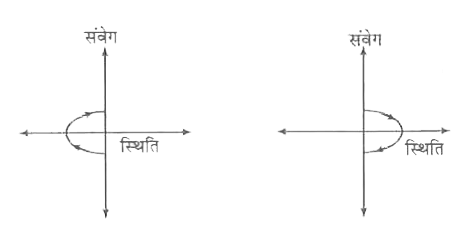
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक दीर्घवृत्त जिसका केन्द्र मूलबिंदु पर है, की उत्केंद्रता 12 है। यदि उसकी एक नियता x=-4 है, तो उसके बिन्दु (1,32) पर उसके अभिलम्ब का समीकरण है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
View Solutionदीर्घवृत्त x236+y29=1 की जीवा का समीकरण, जोकि बिन्दु (2, 1) से जाती है, तथा यह बिन्दु जीवा को दो बराबर-बराबर भागों में विभाजित करता है, होगा
View Solutionअतिपरवलय 25x2−16y2=400 की जीवा का समीकरण क्या होगा, जिसका मध्य बिन्दु (5,3) है ?
View Solutionबिन्दु (1,1) पर वक्रों y=x2 और x=y2 के मध्य कोण है
View Solution
