नीचे दी गई प्रत्येक सरल आवर्त गति के लिए तदनरूपी निर्देश वृत्त का आरेख खींचिए। घूर्णी कण की आरंभिक (t =0) स्थिति, वृत्त की त्रिज्या तथा कोणीय चाल दर्शाइए। सुगमता के लिए प्रत्येक प्रकरण में परिक्रमण की दिशा वामावर्त लीजिए। (x को cm में तथा को में लीजिए।)
(a)x=-2sin (3t+π/3)
(b)x=cos(π6−t)
(c)x=3sin(2πt+π/4)
(d) x=2cosπt
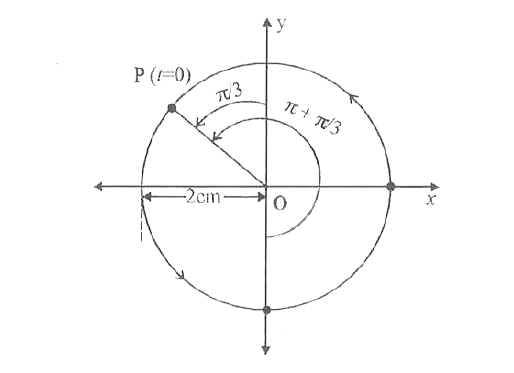
(a) दिये गये समीकरण से
x=−2sin(3t+π+π3) .....(1)
समीकरण (1) की तुलना x=Asin(ωt+ϕ) से करने पर
ϕ+π+π3=4π3,A=2cm.ω=3 रेडियन/से,
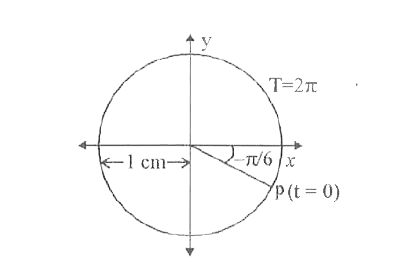
(b) x=cos(π6−t)=cos(t−π6)
[∵cos(−θ)=cosθ]
x=1cos(t−π6).....(2)
तदनुरूपी निर्देश वृत्त को चित्र में दर्शाया गया है। समीकरण (2) की तुलना निम्न समीकरण से करने पर
x=Acos(t−π6).....(3)
A = 1सेमी,
ω=1 रेडियेन/से., T=2π से तथा ϕ=−π6 प्राप्त करते हैं।
अतः दी गई समीकरण निम्न वृत्त आरेख के द्वारा व्यक्त कर सकते
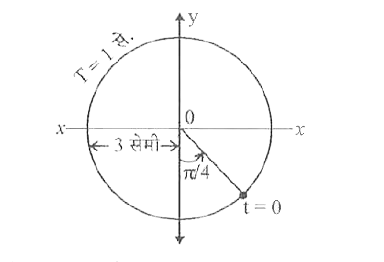
(c) x=3sin(2π+π4) सेमी....(4)
समीकरण (4) की तुलना x=Asin(ωt+ϕ) से करने पर आयाम A= 3 सेमी.,ω=2π
T=2πω=1
ϕ=−π4
तदनुरूपी निर्देश वृत्त को नीचे चित्र में दर्शाया गया है,
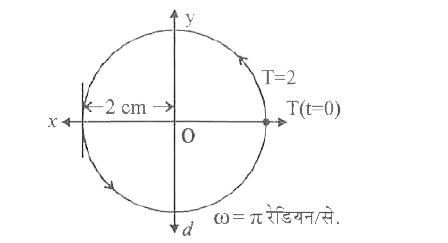
(d) x=2cosπt
=2cos(πt+0) सेमी.....(5)
तदनुरूपी निर्देश वृत्त को चित्र में दर्शाया गया है। समीकरण (5) की तुलना x=Acosωt से करने पर
A = 2 सेमी.,omega=pi, T=2 से., ϕ=0 प्राप्त करते हैं।
Topper's Solved these Questions
- दोलनBOOK - SANJEEV PUBLICATIONCHAPTER - दोलनEXERCISE - अन्य महत्वपूर्ण प्रश्न(बहुचयनात्मक प्रश्न)
31 Videos
- दोलनBOOK - SANJEEV PUBLICATIONCHAPTER - दोलनEXERCISE - अन्य महत्वपूर्ण प्रश्न(रिक्त स्थानों की पूर्ति कीजिए)
10 Videos
- दोलनBOOK - SANJEEV PUBLICATIONCHAPTER - दोलनEXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न
31 Videos
- तरलों के यांत्रिकी गुणBOOK - SANJEEV PUBLICATIONCHAPTER - तरलों के यांत्रिकी गुणEXERCISE - गत वर्षो की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न
57 Videos
- द्रव्य के तापीय गुणBOOK - SANJEEV PUBLICATIONCHAPTER - द्रव्य के तापीय गुणEXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न
81 Videos
Similar Questions
सरल आवर्त गति में प्रत्यानयन बल किसके अनुक्रमानुपाती होता है?
View Solutionधनुष पर प्रत्यंचा चढ़ाकर बाण छोड़ना_____कहलाती है।
View Solutionदो विस्थापनों y1 = a sin (ωt) तथा y = b cos (Ot) के अध्यारोपण से प्राप्त परिणामी गति--
View Solutionझील की तली की गहराई से आधी गहराई पर स्थित किसी बिन्दु पर दाब झील की तली पर दाब का 2/3 है। झील की गहराई होगी
View Solutionएक धात्विक लोलक की घड़ी 0∘C पर सही समय दर्शाती है। यहद एक दिन में 25∘C पर 12.5 संकण्ड मंद हो जाती है, तब धात्विक लोलक का रैखिक प्रसार गुणांक होगा
View Solutionरेखाओ y=mx+c तथाxa+yb=1 को xcosα+ysinα=p के रूप में लिखिए की लंब की लम्बाई ज्ञात कीजिये ।
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solution[0,π] अन्तराल में f(x)=exsinx के लिए रॉले प्रमेय के 'c' का मान होगा
View Solutionनिम्नलिखित संख्याओं में से प्रत्येक को अभाज्य गुणनखंडो की घातों के गुणनफल के रूप में व्यक्त कीजिए -
5400
View Solutionनिम्नलिखित संख्याओं में से प्रत्येक को अभाज्य गुणनखंडो की घातों के गुणनफल के रूप में व्यक्त कीजिए -
8575
View Solutionनिम्नलिखित संख्याओं में से प्रत्येक को अभाज्य गुणनखंडो की घातों के गुणनफल के रूप में व्यक्त कीजिए -
34300
View Solutionप्राथमिक स्तर पर पढ़ने की क्षमता के आकलन में सबसे कम महत्वपूर्ण है
View Solutionsinxx की Limit का अभ्यास [x→0] के लिए
View Solution
