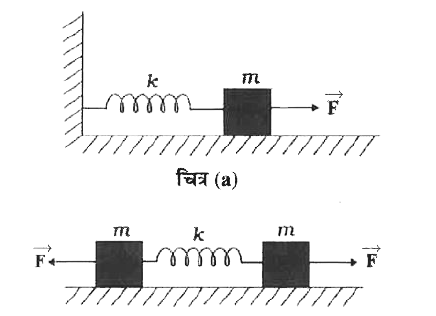
चित्र (a) में k बल-स्थिरांक की किसी कमानी के एक सिरे को किसी दृढ़ आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के मुक्त सिरे पर बल F आरोपित करने से कमानी तन जाती है। चित्र (b) में उस कमानी के दोनों मुक्त सिरों से द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के दोनों सिरों को चित्र (b) में समान बल Fद्वारा तानित किया गया है।
(a) दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या होगा?
(b) यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन काआवर्तकाल ज्ञात कीजिए।
दिया गया है
k = कमानी का बल नियतांक
m = मुक्त सिरों पर द्रव्यमान
F = कमानी के मुक्त सिरों पर उत्पन्न बल
स्थिति।
(a) F = ma ….(1)
यदि कमानी में उत्पन्न विस्तार y1 है
तब F=−ky1....(2)
∴ समीकरण (1) तथा (2) से
ma=−ky1
md2ydt2=−kY1∵a=d2ydt2
d2ydt2=−kmy.....(3)
यहाँ पर विस्थापन y=y1 है।
a=−ω2y....(4)
समीकरण (3) तथा (4) से
w=√km प्राप्त करते हैं....(5)
∴ डोरी में उत्पन्न अधिकतम विस्तार
y1=y
या y1=Fk
(b) समीकरण (4) से हम देखते हैं कि a∝y है और द्रव्यमान S.H.M. कर रहा है।
∴ यदि द्रव्यमान m का दोलनकाल T1 है तब,
t1=2π√mk∵ω=√km
T1=2π√mk....(6)
स्थिति II
(a) माना कमानी में उत्पन्न विस्तार का मान y2 है, जब दोनों द्रव्यमानों को जोड़ा जाता है। क्योंकि द्रव्यमान समान है। यहाँ पर प्रत्येक द्रव्यमान से y विस्तार उत्पन्न किया जाता है y2=y‘+y‘=2y‘.....(7)
y2=Fk
∴Fk=2y‘
या y‘=½Fk
अर्थात् प्रत्येक द्रव्यमान का विस्थापन
y‘=½Fk
y2=2F2k=Fk
[∴y2=2y‘ समीकरण (7) से]
∴ प्रत्येक द्रव्यमान में उत्पन्न त्वरण, तब
d2y1dt2=−Fm=−2ky3m
लेकिन S.H.M. में
d2y3dt2=−ω2y1
ω=√2km
(b) यदि प्रत्येक द्रव्यमान का दोलनकाल T, है तब
T2=2πω
T2=2π√m2k
Topper's Solved these Questions
- BOOK - SANJEEV PUBLICATIONCHAPTER - दोलनEXERCISE - अन्य महत्वपूर्ण प्रश्न(बहुचयनात्मक प्रश्न)31videos
दोलन
- BOOK - SANJEEV PUBLICATIONCHAPTER - दोलनEXERCISE - अन्य महत्वपूर्ण प्रश्न(रिक्त स्थानों की पूर्ति कीजिए)10videos
दोलन
- BOOK - SANJEEV PUBLICATIONCHAPTER - दोलनEXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न31videos
दोलन
- BOOK - SANJEEV PUBLICATIONCHAPTER - तरलों के यांत्रिकी गुणEXERCISE - गत वर्षो की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न57videos
तरलों के यांत्रिकी गुण
- BOOK - SANJEEV PUBLICATIONCHAPTER - द्रव्य के तापीय गुणEXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न81videos
द्रव्य के तापीय गुण
Similar Questions
सरल आवर्त गति में प्रत्यानयन बल किसके अनुक्रमानुपाती होता है?
04:10View Solutionधनुष पर प्रत्यंचा चढ़ाकर बाण छोड़ना_____कहलाती है।
View Solutionदो विस्थापनों y1 = a sin (ωt) तथा y = b cos (Ot) के अध्यारोपण से प्राप्त परिणामी गति--
01:20:52View Solutionझील की तली की गहराई से आधी गहराई पर स्थित किसी बिन्दु पर दाब झील की तली पर दाब का 2/3 है। झील की गहराई होगी
02:17View Solutionएक धात्विक लोलक की घड़ी 0∘C पर सही समय दर्शाती है। यहद एक दिन में 25∘C पर 12.5 संकण्ड मंद हो जाती है, तब धात्विक लोलक का रैखिक प्रसार गुणांक होगा
02:30View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
49:57View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता हैView Solutionस्प्रिंग (कमानी) द्रव्यमान निकाय की सरल आवर्त गति
View Solutionविद्युत सेल के घन सिरे को कौनसी लाइन से व्यक्त करते है
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionवजनी मशीन | कमानी तुला | कमानी की कटाई | श्रेणी और समानांतर कमानी संयोजन
View Solutionचित्र में दर्शाये अनुसार एक आदर्श गैस के एक मोल को A→B अनुसार लिया गया है। प्रक्रम में निहित कार्य का परिमाण है: (R=253JmolK)
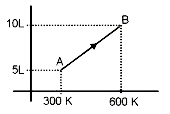 View Solution
View Solutionरुद्धोष्म और समतापीय स्थितियों के तहत एक आदर्श गैस का उत्क्रमणीय प्रसार चित्र में दिखाया गया है | निम्नलिखित में से कौन सा कथन अशुद्ध है
View Solutionनिम्नलिखित में से किन कार्बनिक यौगिकों के नाम को सही ढंग से नहीं लिखा गया है ?
View Solutionएक आदर्श गैस के लिए चक्र के सिरों पर दिखाए गए परिवर्तन की एक श्रेणी के माध्यम से किया गया कुल कार्य निम्न के बराबर है:
View Solutionनिम्नलिखित में से कौन सी नाम अभिक्रिया एक -COOH समूह को निरूपित करने के लिए उपयोग नहीं की जाती है?
View Solution

