वृत्ताकार चाप वाले एक गुटके का द्रव्यमान M है। ये गुटका एक घर्षण रहित मेज पर स्थित है। मेज के सापेक्ष्य (in a coordinate system fixed to the table) गुटके का दाहिना कोर (right edge) x-0 पर स्थित है। द्रव्यमान m वाले एक बिन्दु कण (point mass) को वृत्ताकार चाप के उच्चतम बिन्दु से विरामावस्था से छोड़ा जाता (released from rest) है। ये । बिन्दु कण वृत्ताकार पथ पर नीचे की ओर सरकता है। जब बिन्दु कण गुटके से सम्पर्क विहीन हो जाता है, तब उसकी तात्क्षणिक स्थिति x और गति । है। निम्न में से कौन-सा/से कथन सही है/हैं?
(a) बिन्दु कण (m) का वेग v=
⎷2gR(1+mM)है
(b) गुटके (M) के संहति केन्द्र के विस्थापन का x घटक (x-coordinate) =mRM+m
(c) बिन्दु कण (m) का स्थान x=−√2mRM+m है
(d) गुटके (M) का वेग V=−mM√2gR
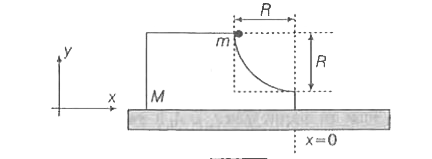
a,b ब्लॉक का ΔXcmrm तथा बिन्दु द्रव्यमान निकाय = 0
∴ m(x + R)+ Mx =0
जहाँ x ब्लॉक का विस्थापन है।
समीकरण को हल करने पर,
X=−mRM+m
संवेग व यान्त्रिक के संरक्षण के संयुक्त निकाय के लिए
0 = my - MV
mgH=12mV2+12MV2
उपरोक्त दोनों समीकरणों को हल करने पर
∴ v=
⎷2gR1+mM
Topper's Solved these Questions
- सॉल्व्ड पेपर 2017 JEE ADVANCEDBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 1 (खण्ड-2)
5 Videos
- सॉल्व्ड पेपर 2017 JEE ADVANCEDBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 1(खण्ड-3)
6 Videos
- सॉल्वड पेपर्स 2021BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर्स 2021EXERCISE - PHYSICS (SECTION B)
19 Videos
- स्थिर वैघुतिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
Similar Questions
एक हाइड्रोजन परमाणु का एक इलेक्ट्रॉन n1 क्वांटम संख्या (quantum number) वाले कक्ष से, ntक्वांटम संख्या (quantum number) के कक्ष में प्रवेश करता है। v1 तथा vt प्राथमिक एवं अन्तिम स्थितिज ऊर्जाएँ है। यदि v1vt=6.25, तब Nt की न्यूनतम सम्भावी संख्या (smallest possiblennt,) है।
View Solutionकिसी स्थिति में कण सीधी रेखा में ऋणात्मक y-अक्ष (negative y-axis) की दिशा में चलेगा?

View Solution10ms−1 वेग से गतिमान 4 kg द्रव्यमान की गेंद किसी 8 m लम्बी स्प्रिंग से टकराती है। स्प्रिंग का बल नियतांक 100Nm−1 है। संपीडित स्प्रिंग की लम्बाई x मीटर है। x का मान निकटतम पूर्णांक में ____ होगा।
View Solutionनाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
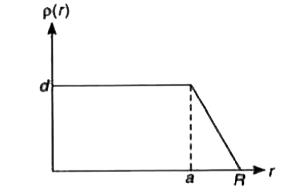
दूरी r= R पर वैघुत क्षेत्र है।
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionबिन्दु (-1,0) से होकर जाने वाले और y-अक्ष को (0,2) पर स्पर्श करने वाला वृत्त निम्न बिन्दु से भी होकर जाता है ।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionबिन्दु (1, 2) से दीर्घवृत्त 3x2+2y2=5 पर खींची गई स्पर्शी युग्मों के बीच का कण है
View Solutionयदि बिन्दु (a,a) रेखाओं |2x+y|=5 के मध्य स्थित है , तब सबसे उपयुक्त एक विकल्प का चयन कीजिए|
View Solution
