एक पतले गोलीय कोश(Shell) का केंद्र उद्गम पर है व् त्रिज्या R है उस पर धनकोष इस प्रकार वितरित है की पृष्ट घनत्व एकसमान है वैघुत क्षेत्र के मान और वैघुत क्षेत्र के मान |E(r)| और वैघुत-विभव V(r) का, केंद्र से दुरी r के साथ बदलाव का सर्वोच्तम वर्णन किस ग्राफ में हे ?
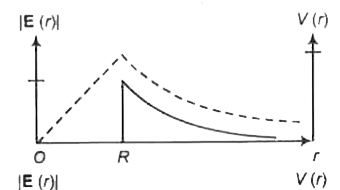
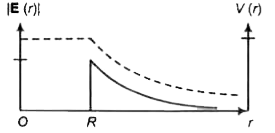
The correct Answer is:D
अंत: बिन्दुओ के लिए
E=0
बाह्य बिन्दुओ के लिए
या
तथा
सतह पर (r=R)
जहाँ पृष्ट आवेश घनत्व
ऊपर दी गयी समीकरणों के अनुसार (d) विकल्प सही आरेख दर्शाता है
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - बहुविकल्पीय प्रश्न II (एक से अधिक विकल्प सही है)15videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - सत्य/असत्य6videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 2(खण्ड-3)4videos
सॉल्व्ड पेपर 2017 JEE ADVANCED
Similar Questions
एक समान्तर प्लेट वायु संघारित्र एक बैटरी से जुड़ा है। इससे सम्बन्धित राशियोँ आवेश, विभव, वैह्युत क्षेत्र तथा ऊर्जा क्रमश: Q0,V0,E0 तथा U0 से प्रदर्शित हैं प्लेटों के बीच पूरे स्थान की भरने के लिए एक परावैद्युत पट्टी खिसकाई जाती है जबकि बैटरी अभी भी जुड़ा है अब राशियाँ Q, V, E तथा, U पूर्व राशियों से सम्बन्धित होंगी
09:03View Solutionकिसी वैद्युत क्षेत्र में एक बिन्दु आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में किया गया कार्य उस पथ पर निर्भर करता है जिसके अनुदिश बिन्दु आवेश ले जाया जाता है।
05:04View Solutionएक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया है। प्रक्रम 1 (Process1) t= 0 पर स्विच S द्वारा परिपथ पूर्ण किया जाता है एवं संधारित्र पूर्ण रूप से वोल्टता V0 से आवेशित हो जाता है। (T» RC समय तक आवेषण चलता रहता है। इस प्रक्रम में प्रतिरोध के द्वारा कुछ विद्युत-कर्जा क्षय (energy dissipated) ED होती है। पूर्ण रूप से आवेशित संधारित्र में संचित ऊर्जा (stored energy in a charged capacitor) का मान EC है।
Q प्रक्रम 1, में संधारित्र में संचित ऊर्जा EC और प्रतिरोध R द्वारा ऊर्जा क्षय E0में सम्बनध है।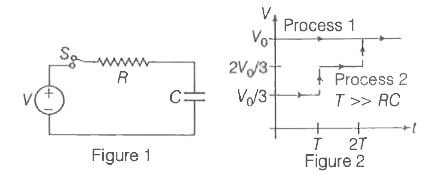
04:01View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?02:29View Solutionआकृति में O वृत्त का केंद्र है। यदि ∠APB=70∘ तो ∠AQB का मान है -
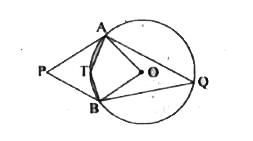06:39View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।03:05View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
01:02View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
01:18:11View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
38:22View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
View Solutionधारावाही वृत्ताकार लूप और कुंडली के केंद्र पर चुंबकीय क्षेत्र
04:19View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionपद्माकर के तीसरे कवित्त में किस ऋतु का वर्णन है ?
View SolutionRs. 2100 is divided among in P , Q and R in such a way that P’s share is half of the combined share of Q and R , and Q’s share is one-fourth of the combined share of P and R. By what amount is R’s share more than that of P? 2100 को P, Q और R में इस तरह से विभाजित किया गया है कि P का हिस्सा Q और R के संयुक्त हिस्से का आधा है और Q का हिस्सा P और R के संयुक्त हिस्से का एक-चौथाई हिस्सा है। R की हिस्सेदारी P की हिस्सेदारी से कितना अधिक है?
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View SolutionNH_3 के साथ अभिक्रिया करने पर एक कार्बनिक यौगिक A, B का निर्माण करता है। गर्म करने पर B, C का निर्माण करता है। KOH की उपस्थिति में C,Br_2 के साथ अभिक्रिया करके CH_3CH_2NH_2 का निर्माण करता है। A है
View Solution