एक त्रिज्या R1 तथा एकसमान आवेश घनत्व का गोलाकार आवेश मूलबिन्दु O पर केन्द्रित है। इसमें एक R2 त्रिज्या तथा P पर केन्द्रित एक गौलाकार गुहिका (cavity), जहाँ OP=a =R1−R2 है, बनाई जाती है। (चित्र देखें)। यदि गुहिका के अन्दर स्थिति r पर विद्युत क्षेत्र E(r) है, तब सही कथन है (हैं)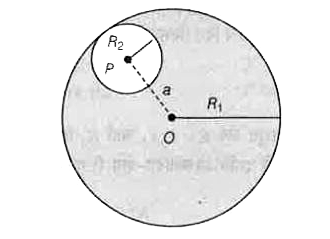 
E एकसमान है, इसका परिमाण R2 पर निर्भर नहीं करता है लेकिन इसकी दिशा पर निर्भर करती है।
E एकसमान है, इसका परिमाण R2 पर निर्भर करता है तथा इसकी दिशा। पर निर्भर करती है।
E एकसमान है, इसका परिमाण 4 पर निर्भर नहीं करता है लेकिन इसकी दिशा a पर निर्भर करती है।
E एकसमान है एवं इसका परिमाण तथा दिशा दोनों a पर निर्भर करते है
The correct Answer is:C
रिक्त स्थान (गुहिका) वाले गोले को R1 त्रिज्या का धनात्मक आयेश वाला पूर्ण गोला माना जा सकता है तथा R2 त्रिज्या व ऋणात्मक आवेश वाले गोले का अन्य पूर्ण गोला माना जा सकता है।
E+→E (धनात्मक आवेश के कारण)
E_(−)→E (ऋणात्मक आवेश के कारण)
E=E++E−
यदि हम इसकी P पर गणना करें तो E− शून्य होगा।
∴E=E+
तथा E+=14πε0qR31 (OP), (OP दिशा में)
जहाँ, q = पूर्ण गोले पर धनात्मक आवेश इसकी दिशा OP या a की अनुदिश है। अतः गुहिका के अन्दर किसी भी बिन्दु पर वैद्युत क्षेत्र नियत रहता है। यह एक मानक परिणाम है।
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - बहुविकल्पीय प्रश्न II (एक से अधिक विकल्प सही है)15videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - स्थिर वैघुतिकीEXERCISE - सत्य/असत्य6videos
स्थिर वैघुतिकी
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्व्ड पेपर 2017 JEE ADVANCEDEXERCISE - पेपर 2(खण्ड-3)4videos
सॉल्व्ड पेपर 2017 JEE ADVANCED
Similar Questions
एक समान्तर प्लेट वायु संघारित्र एक बैटरी से जुड़ा है। इससे सम्बन्धित राशियोँ आवेश, विभव, वैह्युत क्षेत्र तथा ऊर्जा क्रमश: Q0,V0,E0 तथा U0 से प्रदर्शित हैं प्लेटों के बीच पूरे स्थान की भरने के लिए एक परावैद्युत पट्टी खिसकाई जाती है जबकि बैटरी अभी भी जुड़ा है अब राशियाँ Q, V, E तथा, U पूर्व राशियों से सम्बन्धित होंगी
04:35View Solutionकिसी वैद्युत क्षेत्र में एक बिन्दु आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में किया गया कार्य उस पथ पर निर्भर करता है जिसके अनुदिश बिन्दु आवेश ले जाया जाता है।
02:10View Solutionएक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया है। प्रक्रम 1 (Process1) t= 0 पर स्विच S द्वारा परिपथ पूर्ण किया जाता है एवं संधारित्र पूर्ण रूप से वोल्टता V0 से आवेशित हो जाता है। (T» RC समय तक आवेषण चलता रहता है। इस प्रक्रम में प्रतिरोध के द्वारा कुछ विद्युत-कर्जा क्षय (energy dissipated) ED होती है। पूर्ण रूप से आवेशित संधारित्र में संचित ऊर्जा (stored energy in a charged capacitor) का मान EC है।
Q प्रक्रम 1, में संधारित्र में संचित ऊर्जा EC और प्रतिरोध R द्वारा ऊर्जा क्षय E0में सम्बनध है।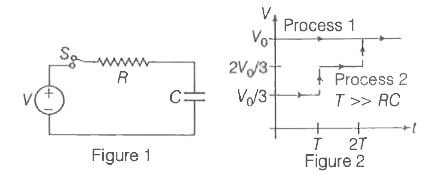
07:40View Solutionदो पासो कि एक युगपत फेक में P (A या B ) का मान ज्ञात कीजिए। यदि A का अर्थ है "पासो पर योगफल 11 प्राप्त करना" तथा B का अर्थ है " प्रत्येक पासे पर एक सम संख्या, एक विषम संख्या है।"
04:01View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
03:14View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
04:32View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।03:50View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
04:26View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
04:29View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
06:39View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
02:42View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
45:46View Solutionकिसी एक विषय पर सर्वांगपूर्ण तथा सम्यकलिखित विचार ------ कहलाता है।
View Solutionकिसी एक विषय पर सर्वांगपूर्ण तथा सम्यकलिखित विचार कहलाता है।
View Solution