अपरिमित लम्बाई और R त्रिज्या के एक ठोस बेलन पर एकसमान आयतन-आवेश घनत्व p है। इसमें R/2 त्रिज्या का खोखला गोलीय-कोश बेलन के अक्ष पर केन्द्रित है (चित्र देखिए) । अक्ष से 2R दूरी पर स्थित बिन्दु P पर विद्युत 23ρR16Kε0 से दिया जाता है। तब व का मान क्या है? 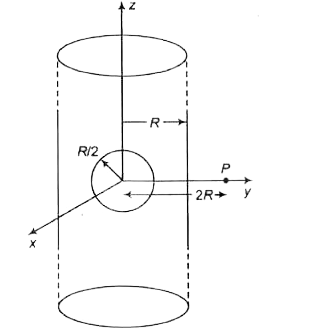
The correct Answer is:K=6
बेलन की प्रति इकाई लम्बाई (l=1) का आयतन
V=πR2l=πR2
अंत: एकांक आवेश
λ=(एकांक आयतन)×(आयतन आवेश घनत्व)
=(πR2p)
अब P पर ER=ET−EC
R= शेष भाग, T= कुल भाग तथा C=गुहिका
ER=λ2πε0(2R)−14πε0Q(2R)2
Q=गोले पर आवेश
=43π(R2)3p=πR3p6
उपरोक्त मान रखने पर ER=(πR2p)4πε0R−14πε0.(πR3p/6)4R2
=23pR96ε0=23pR(16)(6)ε0
k=6
Topper's Solved these Questions
- स्थिर वैघुतिकीBook:JEE Main & Advanced (Hindi Medium)Chapter:स्थिर वैघुतिकीExercise:विश्लेषणात्मक प्रश्न
Explore 22 Videos
- स्थिर वैघुतिकीBook:JEE Main & Advanced (Hindi Medium)Chapter:स्थिर वैघुतिकीExercise:श्रृंखलाबद्ध-बोधन प्रकार
Explore 3 Videos
- स्थिर वैघुतिकीBook:JEE Main & Advanced (Hindi Medium)Chapter:स्थिर वैघुतिकीExercise:मैट्रिक्स-सुमेल प्रकार
Explore 1 Video
- सॉल्व्ड पेपर 2017 JEE ADVANCEDBook:JEE Main & Advanced (Hindi Medium)Chapter:सॉल्व्ड पेपर 2017 JEE ADVANCEDExercise:पेपर 2(खण्ड-3)
Explore 4 Videos
Similar Questions
एक आवेश Q दो संकेन्द्री खोखले गोलों पर जिनकी त्रिज्याएँ r तथा R(>P) हैं, इस प्रकार वितरित है कि उनके पृष्ठ घनत्व (surface densities) बराबर हैं। उभयनिष्ठ केन्द्र पर विभव ज्ञात कीजिए।
View Solutionनाभिकीय आवेश (Ze), R त्रिज्या वाले नाभिक के भीतर असमान रूप से वितरित रहता हैं। आवेश घनत्व p(r) (अर्थात् एकांक आयतन में आवेश की मात्रा) नाभिक के केन्द्र से त्रिज्य दूरी (r) पर ही निर्भर करता है। वैद्युत क्षेत्र त्रिज्य दिशा के अनुदिश है।
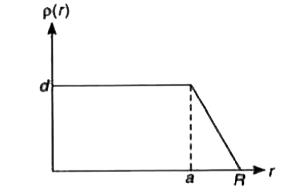
दूरी r= R पर वैघुत क्षेत्र है।
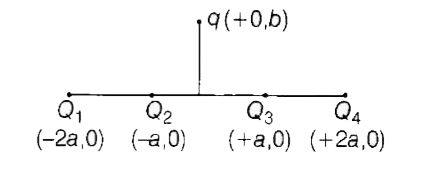
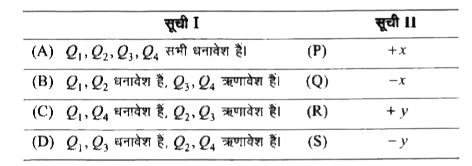
View Solutionचार आवेश Q1,Q2,Q3 तथा Q4, जिनके मान समान हैं, x-अक्ष के अनुदिश क्रमश: x=- 2a, -a,+a तथा +2a पर रखे हैं। एक अन्य घनावेश q+y- अक्ष पर b>0 दूरी पर रखा है। आवेशों के चिह्न (sign) विकल्प सूची । में दिए हैं आवेश पर लगने वाले बलों की दिशा सूची II में दी गई है। सूची I को सूची II से सुमेलित कीजिए तथा सूचियों के नीचे दिये गए कोड का प्रयोग करके सही विकल्प चुनिए
View Solutionएक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया है। प्रक्रम 1 (Process1) t= 0 पर स्विच S द्वारा परिपथ पूर्ण किया जाता है एवं संधारित्र पूर्ण रूप से वोल्टता V0 से आवेशित हो जाता है। (T» RC समय तक आवेषण चलता रहता है। इस प्रक्रम में प्रतिरोध के द्वारा कुछ विद्युत-कर्जा क्षय (energy dissipated) ED होती है। पूर्ण रूप से आवेशित संधारित्र में संचित ऊर्जा (stored energy in a charged capacitor) का मान EC है।
Q प्रक्रम 1, में संधारित्र में संचित ऊर्जा EC और प्रतिरोध R द्वारा ऊर्जा क्षय E0में सम्बनध है।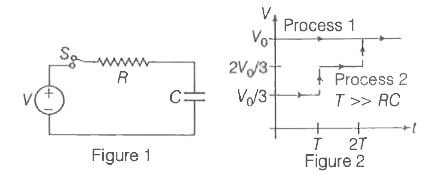
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionमाना PQ और RS,r त्रिज्या के वृत्त के व्यास के सिरों पर खींची गई स्पर्शियाँ है। यदि PS और RQ परिधि पर स्थिति बिन्दु X पर प्रतिच्छेद करते है तो 2r बराबर है-
View Solutionयदि वृत्त x2+y+6x+6y=2 के बिन्दु P पर खींची गई स्पर्शी सरल रेखा 5x−2y+6=0 से y-अक्ष के बिन्दु Q पर मिलती है, तो PQ की लम्बाई है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionउन रेखाओं का समीकरण जिन पर मूल बिन्दु से डाला गया। लम्ब x-अक्ष के साथ 30∘ का कोण बनाता है और उनसे तथा x-अक्ष से बने त्रिभुज का क्षेत्रफल 50√3 वर्ग इकाई हो, है
View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solution