निम्नलिखित व्यवरोधों के अंतर्गत का अधिकतमीकरण कीजिए
The correct Answer is:Z का अधिकतम मान 1800 है जो बिंदु ( 30,0) पर है।
Step by step video, text & image solution for निम्नलिखित व्यवरोधों के अंतर्गत Z = 60x+15y का अधिकतमीकरण कीजिए : x+yle 50 , 3x+yle90,x,yge 0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- रैखिक प्रोग्रामन Book:MITTAL PUBLICATIONChapter:रैखिक प्रोग्रामन Exercise:LAST YEAR.S BOARD QUESTIONS
Explore 7 Videos
- रैखिक प्रोग्रामन Book:MITTAL PUBLICATIONChapter:रैखिक प्रोग्रामन Exercise:COMPETITION CORNER
Explore 14 Videos
- रैखिक प्रोग्रामन Book:MITTAL PUBLICATIONChapter:रैखिक प्रोग्रामन Exercise:महत्वपूर्ण बिंदु (Important Points )
Explore 15 Videos
- प्रायिकता एवं प्रायिकता बंटन Book:MITTAL PUBLICATIONChapter:प्रायिकता एवं प्रायिकता बंटन Exercise:CHECK YOUR POTENTIALITY
Explore 15 Videos
- व्यत्क्रम आव्यूह एव रेखिक समीकरणBook:MITTAL PUBLICATIONChapter:व्यत्क्रम आव्यूह एव रेखिक समीकरणExercise:Check Your Potentiality
Explore 10 Videos
Similar Questions
निम्न व्यवरोधों के अंतर्गत सुसंगत हल क्षेत्र उत्तर -पुस्तिका में दर्शाइए :
2x+y≥8,x≥0,y≥0
View Solutionदिये गये चित्र में छायांकित भाग निम्न सुसंगत क्षेत्र को दर्शाता है -
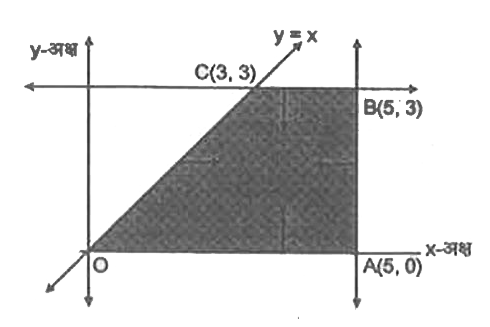
तो प्रतिबन्ध है -
View Solutionनिम्न कथन सत्य है अथवा असत्य-
कुछ व्यवरोधों(constraints) के अंतर्गत किसी रैखिक फलन का न्यूनतम या अधिकतमीकरण करने की विधि को रैखिक प्रोगामान समस्या कहते हैं। रैखिक फलन को उद्देश्य फलन कहते हैं। रैखिक फलन में ऋणेत्तर चार निहित होते हैं।
View SolutionA तथा B दो स्वतंत्र घटनाएँ है , यदि A और B दोनों के एक साथ घटने की प्रायिकता 16 तथा उनमे से किसी के नहीं घटने की प्रायिकता 13 हो , तो A के घटने की प्रायिकता होगी -
View Solutionसमीकरण का नियम जिसके लिए α की वास्तविक मानो की संख्या x+3y+5z=αx,5x+y+3z=αy,3x+5y+z=αz के अनंत हल है-
View SolutionSolve the following linear programming problem graphically:
Maximize : z=60x+15y
Subject to : x+y≤50
3x+y≤90
x≥0
y≥0
View Solutionmaximize z=60x+15y, subject to the constraints x+y≤50,3x+y≤90,x,y≥0.
View Solutionz = 60x + 15y का अधिक्तमीकरण कीजिए, जबकि अवरोध निम्न है-
x+y≤50
3x+y≤90
x≥0
y≥0
View Solutionरैखिक प्रोग्रामिंग इष्टतम मान (अधिकतम या न्यूनतम) को खोजने की एक विधि है जब संबंध रैखिक समीकरणों या असमानताओं के रूप में व्यक्त किया जाता है।
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
निम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
Z=60x+15y
निम्नलिखित व्यवरोध है
x+y≤50
3x+y≤90
x,y≥0
(i)x अक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
(ii)yअक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
(iii) प्रतिच्छेद बिन्दु के निर्देशांक ज्ञात कीजिए
(iv)Z=60x+15y का अधिकतम मान क्या होगा
(v)Z=60x+15y का न्यूनतम मान क्या होगा
View Solutionनिम्न व्यवरोधों के अन्तर्गत Z=3x+2y का न्यूनतमीकरण कीजिए
x+y≥8,3x+5y≤15 तथा x,y≥0
View Solutionव्यवरोधों x+y≤1,x≥0,y≥0,y≥0के अन्तर्गत Z=3x+4y का अधिकतमीकरण कीजिए |
View Solutionव्यवरोधों x≤3,y≤2,x≥0,y≥0के अन्तर्गत फलन Z=11x+7y का अधिकतमीकरण कीजिए |
View Solutionअधिकतमीकरण करें z=60x+15y
जबकि x+y≤50,3x+y≤90,x,y≥0
View Solutionव्यवरोधो x+y≤50,3x+y≤90,x≥0 के अंतर्गत फलन Z=60x+15yका अघिकतम मान ज्ञात कीजिए|
View Solutionनिम्नलिखित व्यवरोधो के अंतर्गत Z=5x+3y का न्यूनतमीकरण कीजिए :
3x+y≥8,x+y≥4,x≥0,y≥0
View SolutionZ=5x+7y का अधिकतमीकरण कीजिए , जबकि व्यवरोध है :
x+y≤4,3x+8y≤24,x,y≥0.
View Solution