रेखीय प्रतिबंधों x+y≤20,x+2y≤35,x−3y≤12 के अंतर्गत 4x+5y का अधिकतम मान है -
84
95
100
96
The correct Answer is:b
Topper's Solved these Questions
- रैखिक प्रोग्रामन BOOK - MITTAL PUBLICATIONCHAPTER - रैखिक प्रोग्रामन EXERCISE - COMPETITION CORNER
14 Videos
- प्रायिकता एवं प्रायिकता बंटन BOOK - MITTAL PUBLICATIONCHAPTER - प्रायिकता एवं प्रायिकता बंटन EXERCISE - CHECK YOUR POTENTIALITY
15 Videos
- व्यत्क्रम आव्यूह एव रेखिक समीकरणBOOK - MITTAL PUBLICATIONCHAPTER - व्यत्क्रम आव्यूह एव रेखिक समीकरणEXERCISE - Check Your Potentiality
10 Videos
Similar Questions
दिये गये चित्र में छायांकित भाग निम्न सुसंगत क्षेत्र को दर्शाता है -
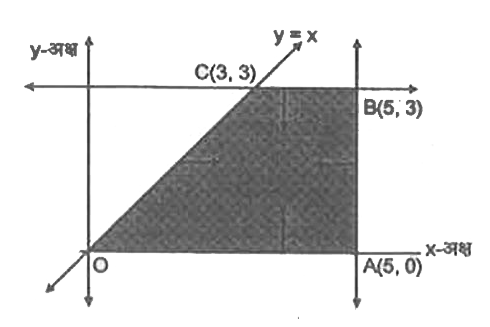
तो प्रतिबन्ध है -
View SolutionA तथा B दो स्वतंत्र घटनाएँ है , यदि A और B दोनों के एक साथ घटने की प्रायिकता 16 तथा उनमे से किसी के नहीं घटने की प्रायिकता 13 हो , तो A के घटने की प्रायिकता होगी -
View Solutionसमीकरण का नियम जिसके लिए α की वास्तविक मानो की संख्या x+3y+5z=αx,5x+y+3z=αy,3x+5y+z=αz के अनंत हल है-
View SolutionThe minimum value of Z= 4x+5y subject to the constraints x≤30,y≤40 and x≥0,y≥0 is
View Solutionयदि फलन f(x) द्वारा अधिकतम मान x व y न्यूनतम मान ग्रहण किया जाता है तो इस फलन का आयाम . . . . . . . है ।
View SolutionThe maximum value of 4x +5y subject to the constraints x+y≤20,x+2y≤35,x−3y≤12 is
View Solutionव्यवरोधों 2x+y≤6,x≤2,x≥0,y≥0के अन्तर्गत Z=11x+7y का अधिकतम मान निर्धारित कीजिए |
View SolutionSolve the following system of inequalities graphically:
x+y≤200,x≤20,y≥4x,x≥0,y≥0.
View Solution352 का मान है-
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionनिम्न समस्या को हल कीजिए :
Z=6x−2y का अधिकतम मान ज्ञात कीजिए जबकि
2x−y≤2,x≤3,x≥0,y≥0
View Solutionनिम्न व्यवरोधों के अंतर्गत Z=x+5y+20 का न्यूनतमीकरण कीजिए :
x−y≥0,−x+2y≥2,x≥3,x0≤y≤4
View Solutionनिम्न व्यवरोधों के अंतर्गत Z=4x+3y का न्यूनतमीकरण कीजिए :
2x+y≥40,x+2y≥50,x+y≥35,x,y≥0
View SolutionZ=15x+10y का निम्न व्यवरोधों के अंतर्गत 3x+y≤600,x+y≤400,x≤200,y≤400,x≥0,y≥0 अधिकतम मान है।
View Solutionव्यवरोधों x+3y≥3,x+y≥2,x≥,y≥0 के अंतर्गत Z=3x+8y का न्यूनतम मान है।
View Solution
