Question

एक R त्रिज्या कि पतली वलय पर q आवेश एक समान रूप से वितरित है वलय कि अक्ष पर केन्द्र से x दूरी स्थित बिंदु पर विधुत क्षेत्र कि तीव्रता ज्ञात कीजिए। प्राप्त परिणाम कि प्रतिबन्ध $x>>R$ के लिए विवेचना कीजिए।

Explanation

वलय पर रेखीय आवेश घनत्व `lamda=(q)/(2piR)` है। वलय पर दो लघु खण्डो 1 और 2 प्रत्येक लम्बाई dl का विचार कीजिये। तब अक्ष पर केन्द्र O से x दूरी पर स्थित बिंदु P पर, इन लघु खण्डो के कारन उत्पन्न विधुत क्षेत्र कि तीव्रता होगी,

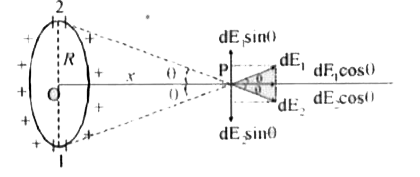
`dE_(1)=dE_(2)=(K lamdadl)/((R^(2)+x^(2)))`
इन विधुत क्षेत्रो कि दिशायें, जबकि क्षैतिज घातक जुड़ जायेंगे। इस प्रकार, हम कह सकते है की वलय के किसी भी एक लघुखण्ड के द्वारा P पर उत्पन्न विधुत क्षेत्र का प्रभावी भाग, उसके क्षैतिज घातक के बराबर होगा, अर्थात
`dE=(k lamdadl)/((R^(2)+x^(2)))costheta`
`=(k lamda" dl x")/((R^(2)+x^(2))^(3/2))`
प्रत्येक वलय से विधुत क्षेत्र, प्रत्येक खण्ड से उत्पन्न विधुत क्षेत्रो के योग से प्राप्त होगा, अर्थात
`E=(klamdax)/((R^(2)+x^(2))^(3/2))intdl`
`=(klamda" x "2piR)/((R^(2)+x^(2))^(3/2))`
या `" "E=(Kqx)/((R^(2)+x^(2))^(3//2))=(qx)/(4pi in_(0)(R^(2)+x^(2))^(3//2))`
प्रतिबन्ध `xgt gt R` के लिए उपरोक्त समीकरण से -
`E=(Kqx)/(x^(3))=(Kq)/(x^(2))`
यह किसी बिन्दु आवेश q से x दूरी पर उत्पन्न विधुत क्षेत्र का व्यंजक है। इस प्रकार अक्ष पर दूर स्थित बिंदुओं के लिए वलय इस प्रकार व्यवहार करती है मानों कि सम्पूर्ण आवेश इसके केन्द्र पर संकेन्द्रित है।