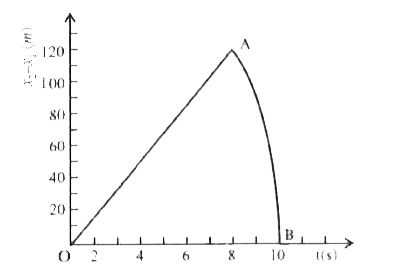
किसी 200 m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15 ms−1 तथा 30 ms−1 की प्रारम्भिक चाल से फेंका जाता है | इसका सत्यापन कीजिए कि सामने दिखाया गया ग्राफ ( चित्र) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है | वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं | मान लीजिए g=10ms−2 | ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए |
पहले पत्थर के t समय के लिए ऊर्ध्वाधर गति लेते हुए
x0=200m,
x0=200m,
u=15m/s,
a=−10m/s2,t=t,x=x1
x=x0+ut+12at2
∴ x1=200+15t+12(−10)t2
x1=200+15t−5t2 ...(1)
दूसरे पत्थर के लिये ऊर्ध्वाधर गति t समय के लिये
x0=200m,u=30m/s.
a=−10m/s2,t=t2x=x2
तब x2=200+30t−12×10t2
x2=200+30t−5t2 ...(2)
जब पहला पत्थर जमीन पर टकराता है|
x1=0
∴ समीकरण (1 ) से
0=200+15t−5t2
⇒ 5t2−15t−200=0
⇒ 5t2−15t−200=0
या t2−3t−20=0
या (t−8)(t+5)=0
∴ t=8 सेकण्ड या t=−5 सेकण्ड
∵ t=−5 सेकण्ड (अर्थहीन है)
∴ t=8 सेकण्ड
दूसरे पत्थर के लिये जब दूसरा पत्थर जमीन से टकराता है
x2=0
इसलिये समीकरण (2 ) से
0=200+30t−5t2
या 5t2−30t−200=0
या t2−6t−40=0
(t−10)(t+4)=0
∴ t=10 सेकण्ड या t=−4 सेकण्ड
∵ t=−4 सेकण्ड (अर्थहीन है)
∴ t=10 सेकण्ड
समीकरण (2 ) व समीकरण (1 )
x2−x1=15t ...(3)
यहाँ पर (x2−x1) और t दोनों ही एकघातीय संबंघ से जुड़ें हैं| इसलिए आरेख एक सरल रेखा होगी|
∴ वक्र का भाग OA एक सरल रेखा t = 8 सेकण्ड पर दोनों पत्थरों के बीच दुरी अधिकतम होगी, क्योंकि पत्थर (1 ) पृथ्वी पर आ जाता है जबकि दूसरा पत्थर गति में रहता है|
x2−x1=15×8=120m
8 सेकण्ड बाद केवल दूसरा पत्थर 2 सेकण्ड के लिए गति में होगा| ग्राफ 8 सेकण्ड से 10 सेकण्ड के बीच द्विघात समीकरण x2=200+30t−5t2 के अनुसार होगा अर्थात यह परवलीय है|
Topper's Solved these Questions
- BOOK - SANJEEV PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अन्य महत्वपूर्ण प्रश्न (बहुचयनात्मक प्रश्न-)16videos
सरल रेखा में गति
- BOOK - SANJEEV PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अन्य महत्वपूर्ण प्रश्न (रिक्त स्थानों को की पूर्ति कीजिए-)10videos
सरल रेखा में गति
- BOOK - SANJEEV PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अभ्यास (पाठ्यपुस्तक के प्रश्न)22videos
सरल रेखा में गति
- BOOK - SANJEEV PUBLICATIONCHAPTER - समतल रेखा में गतिEXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न26videos
समतल रेखा में गति
Similar Questions
एक कण की एकविमीय गति के लिए वेग - समय ग्राफ चित्र के अनुसार है | कण का त्वरण है | (मी./से2 में )-
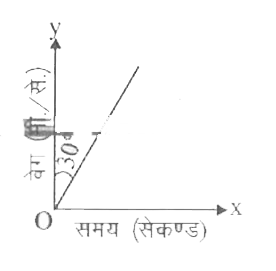 50:12View Solution
50:12View Solutionदो कारों का समय - विस्थापन ग्राफ दो समान्तर रेखाओं से प्रदर्शित होता है | उनके वेगों में ..................................का सम्बन्ध होता है |
03:25View Solutionनीचे दिए गए गति के कौन-से उदाहरणों में वस्तु को लगभग बिंदु वस्तु माना जा सकता है -
दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी |
(b) किसी वृत्तीय पथ पर साईकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर |
(c) जमीन से टकरा कर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद |
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर |View Solutionक्षैतिज घर्षण विहीन टेबिल के केंद्र पर स्थित खूंटी से l लंबाई की डोरी का एक सिरा बांधा गया है तथा दूसरे सिरे पर m द्रव्यमान का एक कण बांधा उसे v वेग से वृत्तीय गति करवाई जाती है कण पर केंद्र की ओर लगने वाला बल होगा (T डोरी में तनाव को दर्शाता है)
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionजब दो तत्वों A और D के दो यौगिकों ACl_(3) और DCl_(3) को एक साथ मिश्रित किया जाता है, तो एक यौगिक ADCl_(6) का निर्माण होता है। संरचनात्मक विश्लेषण से पता चला कि ADCl_(6) एक आयनिक यौगिक है। दिया गया है कि DCl_(3) त्रिकोणीय समतल है और ACl_(3) त्रिकोणीय पिरामिडीय है, ऋणायन DCl_(4)^(-) की आकृति ज्ञात कीजिए।
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionग्लूकोज के ताजा तैयार विलयन से समय के साथ प्रकाशिक घूर्णन में परिवर्तन को निम्न में जाना जाता है -
View Solutionगैस के दाब के साथ ठोस की सतह पर गैसों के अधिशोषण के लिए निम्नलिखित में से सही परिवर्तन है
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution1 M NaOH विलयन के 2.5 लीटर को अन्य 0.5 M NaOH विलयन के 3 लीटर के साथ मिलाया जाता है। परिणामी विलयन की मोलरता है -
View Solutionनिम्नलिखित में से कौनसा आरेख एक प्रबल विद्युत अपघट्य के लिए तनुकरण के साथ तुल्यांकी चालकत्व (A) की सही परिवर्तनशीलता को प्रदर्शित करता है?
View Solutionबेन्जैल्डिहाइड बनाने के लिए AlCl3 की उपस्थिति में बेन्जीन के साथ CO+HCI की अभिक्रिया को क्या कहा जाता है?
View SolutionNaOH की उपस्थिति में, फीनॉल के साथ बेंजॉयल क्लोराइड की अभिक्रिया को कहा जाता है:
View Solution

