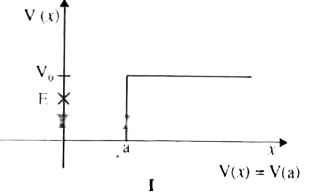
चित्र में कुछ एकविमीय स्थितिज ऊर्जा - फलनों के उदाहरण दिए गए है। कण की कुल ऊर्जा कोटि - अक्ष पर क्रॉस द्वारा निर्देशित की गई है। प्रत्येक स्थिति में , कोई ऐसे क्षेत्र बताइये , यदि कोई है तो , जिनमे दी गई ऊर्जा के लिए , कण को नहीं पाया जा सकता । इसके अतिरिक्त , कण की कुल न्यूनतम ऊर्जा भी निर्देशित कीजिये। कुछ ऐसे भौतिक संदर्भो के विषय में सोचिये जिनके लिए ये स्थितिज ऊर्जा आकृतियाँ प्रासंगिक हो।
हम जानते है की पिण्ड की कुल ऊर्जा E=K.E+P.E
या K.E=E.P.E=12mv2
∵K.E कभी भी ऋणात्मक नहीं हो सकती , अतःP.E का मान सदैव E से कम ही होगा।
(i) x = a और x = 0 के बीच क्षेत्र P.E में शून्य है अतः गतिज ऊर्जा (K.E) धनात्मक है ।
इस स्थिति में कण में न्यूनतम कुल ऊर्जा शून्य है
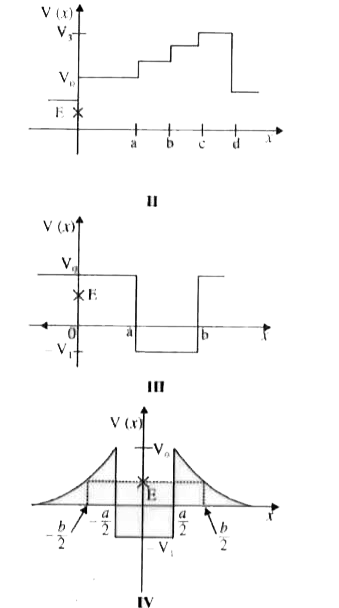
(ii) x = a और x>b के लिए P.E(V0)>E
∴K.E का मान ऋणात्मक होगा। इस कारण से वस्तु x<a और x>b के क्षेत्र में उपस्थित नहीं रह सकती । क्षेत्र x>a तथा x<b में ऋणात्मक है। इसका अर्थ है की गतिज ऊर्जा का मान धनात्मक है इसीलिए क्षेत्र x>a और x<a में कण पाया जा सकता है। इस स्थिति में जो कुल ऊर्जा कण में हो सकती है , वह V1 है।
(iii) कण किसी भी क्षेत्र में दिखाई नहीं देगा चूँकि प्रत्येक क्षेत्र में P.E(V0)>E है।
अतः क्षेत्र −∞<x<∞ में कण उपस्थित नहीं हो सकता है।
इस स्थिति में कण की न्यूनतम ऊर्जा −V1 हो सकती है ।
(iv) इस स्थिति में कण की कुल ऊर्जा उसकी कुल ऊर्जा P.E से अधिक है ।
इसी आधार से क्षेत्र −b2<x<−a2,a2<x<b2 में कण उपस्थित नहीं हो सकता है।
इस प्रकार तीनो क्षेत्रो में गतिज ऊर्जा ऋणात्मक होगी।
इस प्रकार कण इन क्षेत्रो में उपस्थित नहीं होगा।
−b2,x<−a2 तथा a2<x<b2
इस स्थिति में कण की न्यूनतम कुल ऊर्जा −V1 हो सकती है ।
Topper's Solved these Questions
- कार्य ऊर्जा और शक्ति BOOK - SANJEEV PUBLICATIONCHAPTER - कार्य ऊर्जा और शक्ति EXERCISE - अभ्यास के अतिरिक्त प्रश्न -
7 Videos
- कार्य ऊर्जा और शक्ति BOOK - SANJEEV PUBLICATIONCHAPTER - कार्य ऊर्जा और शक्ति EXERCISE - अन्य महत्वपूर्ण प्रश्न ( बहुचयनात्मक प्रश्न )
18 Videos
- कार्य ऊर्जा और शक्ति BOOK - SANJEEV PUBLICATIONCHAPTER - कार्य ऊर्जा और शक्ति EXERCISE - गत वर्षो के विभिन्न प्रतियोगी परीक्षाओ में पूछे प्रश्न
23 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SANJEEV PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न
30 Videos
- गुरुत्वाकर्षण (Gravitation)BOOK - SANJEEV PUBLICATIONCHAPTER - गुरुत्वाकर्षण (Gravitation)EXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न
25 Videos
Similar Questions
0.012 द्रव्यमान की कोई गोली 70ms−1 की क्षैतिज चाल से हुए 0.4kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरंत ही विरामावस्था में आ जाती है। गुटके को छत से पतली द्वारा लटकाया गया है। परिकलन कीजिये गुटका किस ऊँचाई तक ऊपर उठता है ? गुटके में पैदा हुई ऊष्मा की मात्रा भी अनुमान लगाइये।
View Solutionकिसी निकाय पर संरक्षी आंतरिक बल द्वारा किये गए कार्य का ऋणात्मक मान तुल्य होता है -
View Solutionकिसी कण पर (4ˆi+3ˆj)N बल लगाने पर वह बिंदु (−2ˆi+5ˆj) से बिंदु (4ˆj+3ˆk) तक विस्थापित हो जाता है । इस प्रक्रिया में बल द्वारा किया गया कार्य -
View Solutionकिसी एकसमान ठोस शंकु के द्रव्यमान केंद्र की उसके शीर्ष से दूरी z0 हैं । यदि शंकु के आधार की त्रिज्या R तथा शंकु की ऊंचाई h हो तो z0 का मान निम्नांकित में से kiske बराबर होगा -
View Solutionपरस्पर गुरुत्वीय आकर्षण के प्रभाव में दो समान द्रव्यमान कण त्रिज्या Rके वृत्तीय पथ पर गति कर रहे हैं। प्रत्येक कण की चाल होगी
View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
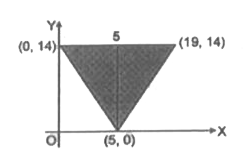
View Solutionस्थिरवैद्युत स्थितिज ऊर्जा, || बाह्य क्षेत्र में द्विध्रुव की स्थितिज ऊर्जा
View Solutionऊर्जा के विभिन्न रूप | यांत्रिक ऊर्जा |गतिज ऊर्जा तथा स्थितिज ऊर्जा | संवेग और गतिज ऊर्जा में सम्बन्ध |किसी स्प्रिंग की स्थितिज ऊर्जा
View Solutionप्राथमिक स्तर पर पढ़ने की क्षमता के आकलन में सबसे कम महत्वपूर्ण है
View Solutionनिर्वात में इलेक्ट्रॉनों को त्वरित करके X-किरणों को उत्पन्न किया जा सकता है और एक धातु के पृष्ठ के परमाणुओं पर उन्हें आपतित किया जाता है। यदि इलेक्ट्रॉनों की 1000 ev गतिज ऊर्जा पूरी तरह से फोटॉन ऊर्जा में परिवर्तित हो जाती है। यदि इलेक्ट्रॉन धारा 1.5 xx 10^(-5) A है, तो 10^(-10) सेकंड में कितने फोटॉन उत्पन्न होते हैं?
View Solutionदी गई अभिक्रिया में, अग्र अभिक्रिया के लिए सक्रियण ऊर्जा (E_a)_f का मान 80 kJmol^(-1) है तथा DeltaH = -40 kJmol^(-1) है। एक उत्प्रेरक, सक्रियण ऊर्जा (E_a)_f " को " 20 kJmol^(-1) तक कम करता है। उत्प्रेरक के योग से पहले तथा बाद में, उत्क्रमणीय अभिक्रिया के लिए सक्रियण ऊर्जा का अनुपात है:
View Solutionएक अभिक्रिया की सक्रियण ऊर्जा को निम्न में से किस ग्राफ की प्रवणता से निर्धारित किया जा सकता है?
View Solutionहाइड्रोजन परमाणु में यदि इलेक्ट्रॉन n = 3 से n = 2 में गिरता है, तो उत्सर्जित ऊर्जा की मात्रा है -
View Solutionदी गई स्पीशीज में से किसका उपयोग फ्रीडेल क्राफ्ट अभिक्रियाओं में नहीं किया जा सकता है?
View Solutionहाइड्रोजन के समान एक काल्पनिक परमाणु के लिए, निकाय की स्थितिज ऊर्जा U (1) = (-ke^2)/(r^3) द्वारा दी जाती है, जहाँ r दो कणों के बीच की दूरी है। यदि कोणीय संवेग के क्वान्टीकरण का बोर मॉडल लागू होता है, तो कण का वेग निम्नलिखत में किसके द्वारा दिया जाता है?
View Solution25^@ C पर, दी गई अभिक्रिया के लिए, नियत आयतन पर, अभिक्रिया की ऊष्मा और आंतरिक ऊर्जा में परिवर्तन के बीच अंतर, kJ में है: 2 C_6 H_6 (l ) + 15 O_2 (g) to 12 CO_2 (g) + 6 H_2 O(l)
View Solution
