इलेक्ट्रॉन के स्थायी कक्षा के लिए त्रिज्या एवं वेग के लिए व्यंजक प्राप्त कीजिए।
अथवा
बोर के अभिगृहीतों के आधार पर हाइड्रोजन परमाणु की nवीं स्थाई कक्षा में इलेक्ट्रॉन के कक्षीय वेग के व्यंजक की व्युत्पत्ति कीजिए। वीं कक्षा में परिभ्रमण करने वाले इलेक्ट्रॉन पर नाभिक द्वारा आरोपित विद्युत आकर्षण
F
e
=
1
4
π
ε
0
Z
e
2
r
2
n
…………..2
यहां Z नाभिक का परमाणु क्र
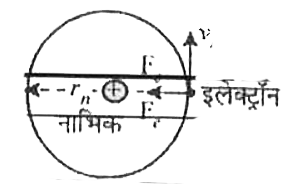
इलेक्ट्रॉन के स्थाई कक्षा की त्रिज्या- माना कि परमाणु का इलेक्ट्रॉन n वीं कक्षा में Vn वेग से परिभ्रमण कर रहा है । इस कक्षा की त्रिज्या rn है । यदि इलेक्ट्रॉन का द्रव्यमान m माना जाये तो इस कक्षा में इलेक्ट्रॉन का कोणीय संवेग mVnrn होगा।
बोर के अनुसार कोणीय संवेग का मान h2π का पूर्ण गुणज होता है अतः
mvnrn=n.h2π………1
n वीं कक्षा में परिभ्रमण करने वाले इलेक्ट्रॉन पर नाभिक द्वारा आरोपित विद्युत आकर्षण
Fe=14πε0Ze2r2n…………..2
यहां Z नाभिक का परमाणु क्रमांक है
n वीं कक्षा में इलेक्ट्रॉन के लिए आवश्यक अभिकेंद्रीय बल
Fe=mV2nrn ……..3
इलेक्ट्रॉन पर नाभिक द्वारा लगने वाला बल ही आवश्यक अभिकेंद्रीय बल प्रदान करता है अतः
Fe=Fe
या 14πε0Ze2r2n=mv2nrn ……….4
समीकरण 1 से
Vn=nh2πmrn……5
समीकरण 5 से Vn का मान समीकरण 4 में रखने पर
14πε0Ze2r2n=mrn×n2h2rπ2m2.r2n
या Ze2ε0=n2h2rn.πm
या rn=ε0n2h2πm.Ze2=.529n2ZA…6
∴ प्रथम कक्षा की त्रिज्या (n=1 रखने पर)
r1=ε0.h2πm.Ze2………7
समीकरण 6 व 7 से
rn=n2×r ……..8
r1 को प्रथम कक्ष की त्रिज्या अथवा परमाणु की बोर त्रिज्या कहते हैं। इसे पंक्ति a0 द्वारा व्यक्त करते हैं जिससे a0=ε0h2πme2
समीकरण 7 से स्पष्ट है कि परमाणु की किसी कक्षा की त्रिज्या कामान बोर त्रिज्या (r1) एवं कक्षा की संख्या वर्ग (n2) के गुणनफल के बराबर होता है।
इलेक्ट्रॉन का कक्षीय वेग- बोर की प्रथम परिकल्पना से
nV2nrn=14πε0Ze2r2n ………..9
द्वितीय परिकल्पना से
mVnrn=nh2π ……..10
समीकरण 9 में 10 का भाग देने पर
Vn=Ze22ε0nh
=2πkZe2nh=(e137).Zn
=2.18×106Zn मी./से.
यहां c= प्रकाश की चाल
=3×108 मी/से
हाइड्रोजन परमाणु के लिए Z=1
∴Vn=e22ε0nh………..11
यदि n=1 हो तो
V1=e22ε0h
अतः Vn=V1n
यहां V1 हाइड्रोजन परमाणु के प्रथम कक्षा के इलेक्ट्रॉन का कक्षीय वेग है।
Topper's Solved these Questions
- परमाणवीय एवं नाभिकीय भौतिकीBOOK - TRIPUTI PUBLICATIONCHAPTER - परमाणवीय एवं नाभिकीय भौतिकीEXERCISE - आंकिक प्रश्न
6 Videos
- परमाणवीय एवं नाभिकीय भौतिकीBOOK - TRIPUTI PUBLICATIONCHAPTER - परमाणवीय एवं नाभिकीय भौतिकीEXERCISE - लघूत्तरात्मक प्रश्न
11 Videos
- धारा वैद्युतिकी BOOK - TRIPUTI PUBLICATIONCHAPTER - धारा वैद्युतिकी EXERCISE - आंकिक प्रश्न
9 Videos
- प्रकाश विधुत प्रभाव एवं द्रव्य तरंगे BOOK - TRIPUTI PUBLICATIONCHAPTER - प्रकाश विधुत प्रभाव एवं द्रव्य तरंगे EXERCISE - एकांकी प्रश्न
8 Videos
Similar Questions
.146C की अर्धआयु 5700 वर्ष है। इसका क्या अर्थ हैं?
View Solutionबोर मॉडल की दो सीमाएं लिखिए।
View Solutionविद्युत वाहक बल तथा 2Ω आन्तरिक प्रतिरोध की एक बैटरी किसी प्रतिरोधक से संयोजित है | इसमें 0.5 A की विद्युत धारा प्रवाहित रही है तो प्रतिरोध ज्ञात कीजिए | यदि परिपथ बन्द है तो सैल की टर्मिनल वोल्टता क्या होगी |
View Solutionसीजियम धातु के लिए देहली आवृत्ति 5.16×10−14Hz है । इसका कार्य फलन eV में ज्ञात कीजिए ।
View Solutionपरमाणु के नाभिक की खोज एवं संघटन|मोजले का प्रयोग
View Solutionपरमाणु के नाभिक की खोज एवं संघटन||मोजले का प्रयोग
View Solutionइलेक्ट्रॉन के आधार पर ऑक्सीकरण एवं अपचयन
View Solutionविशेष क्षमता वाले बच्चो की कक्षा में 'लेखन-कौशल' के अभ्यास के लिए महत्वपूर्ण है
View Solutionहाइड्रोजन परमाणु के लिए बोर मॉडल |प्रश्न|H परमाणु में विभिन्न कोश की ऊर्जा|Summary
View Solutionहाइड्रोजन जैसी कौन सी प्रजाति की त्रिज्या, हाइड्रोजन परमाणु की प्रथम बोर कक्षा की त्रिज्या के समान होगी?
View SolutionLi^(2+) की द्वितीय बोर कक्षा की त्रिज्या (बोर त्रिज्या (a_(0)) के पदों में) (xa_(0))/(y) द्वारा दी जातिही | जहाँ x+y का योग ज्ञात कीजिए -
View Solutionहाइड्रोजन परमाणु के द्वितीय बोर कक्षा में एक इलेक्ट्रॉन की गतिज ऊर्जा है- [ a_(0) हाइड्रोजन परमाणु के प्रथम कोश की बोर त्रिज्या है]
View Solutionनाभिक से दूरी पर, अनंतसूक्ष्म मोटाई dr के गोलीय कोश में हाइड्रोजन परमाणु के 1s इलेक्ट्रॉन के पाए जाने की प्रायिकता P है। इस कोश का आयतन 4rr2 dr है। r पर P की निर्भरता का गुणात्मक रेखाचित्र है-
View Solutionनिम्नलिखित में से कौन सा आरेख एक कक्षा में e^(-) के वेग के विरूद्ध Z, 1/n और n के लिए सही है?
View Solutionएक परमाणु में, दो इलेक्ट्रॉन नाभिक के चारों त्रिज्या r और 4r की वृत्ताकार कक्षाओं में परिक्रमण करते हैं। एक परिक्रमण को पूर्ण करने के लिए उनके द्वारा लिए गए समय का अनुपात (T_2 : T_1) है:
View Solutionहाइड्रोजन परमाणु की निम्नतम कक्षा में इलेक्ट्रॉन की बंधन ऊर्जा 13.6 ev है। हाइड्रोजन की तीन सबसे निम्नतम कक्षाओं की ऊर्जा के परिमाण
View Solution
